Evaluating ∫ 0 π 2 (1 log (tan x) 1 1 − tan (x)) 3 d x Using the method shown here, I have found the following closed form ∫ 0 π 2 (1 log (tan x) 1 1 − tan x) 2 d x = 3 ln 2 − 4 π
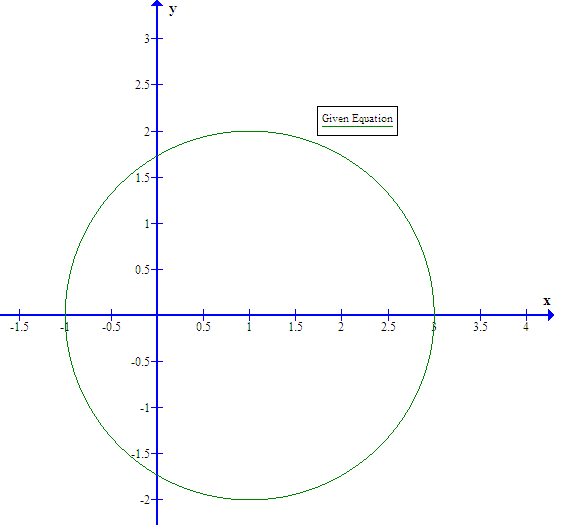
(x^2+y^2-1)^3-Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history "Now for x 2 y 22x4y=0 you can solve in another way You can add both sides with 5 and you 'll get x 2 y 2 2x 4y 5 = 5 and by factorizing you will end up in the form (x
(x^2+y^2-1)^3のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  |  |
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
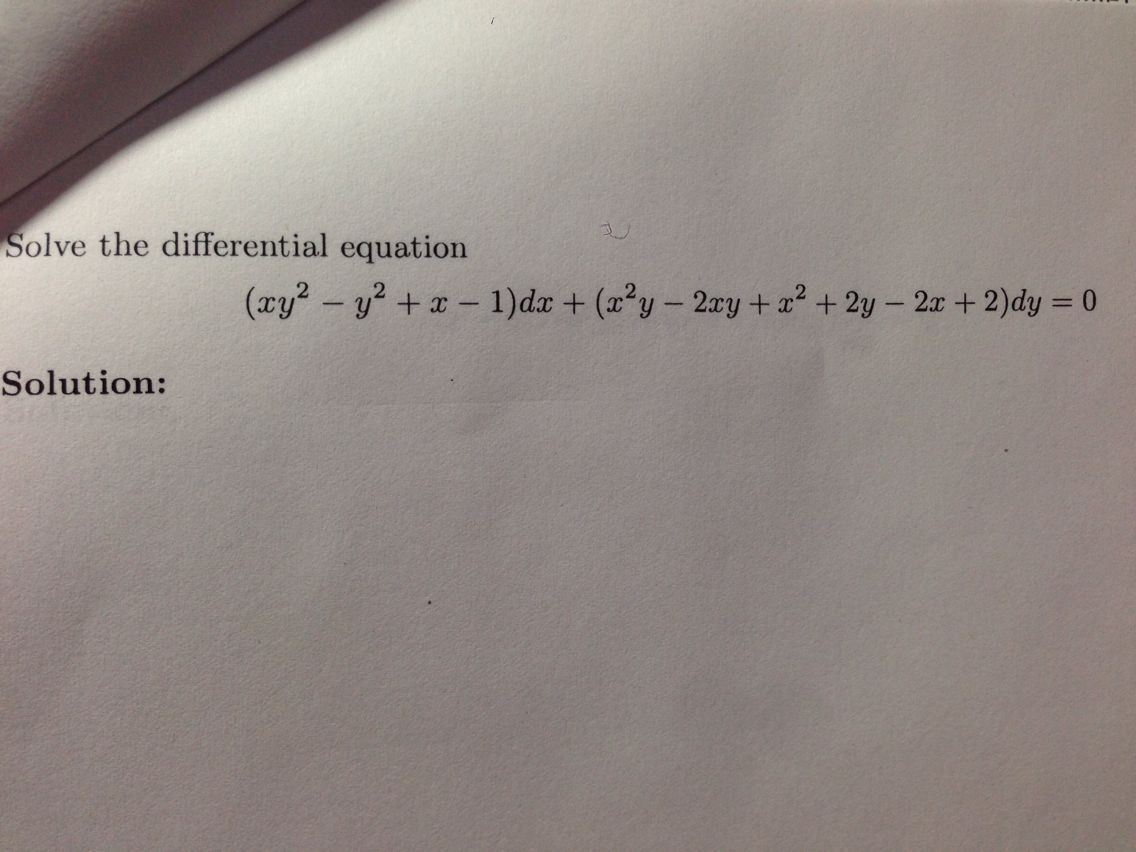 | ||
 |  |  |
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 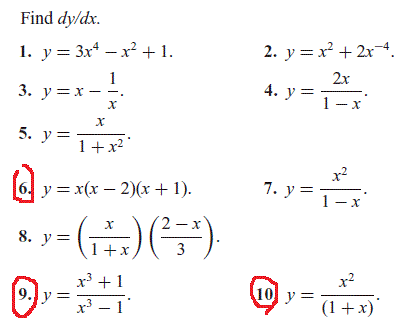 |  |
 |  | |
 |  |  |
 |  | |
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 | 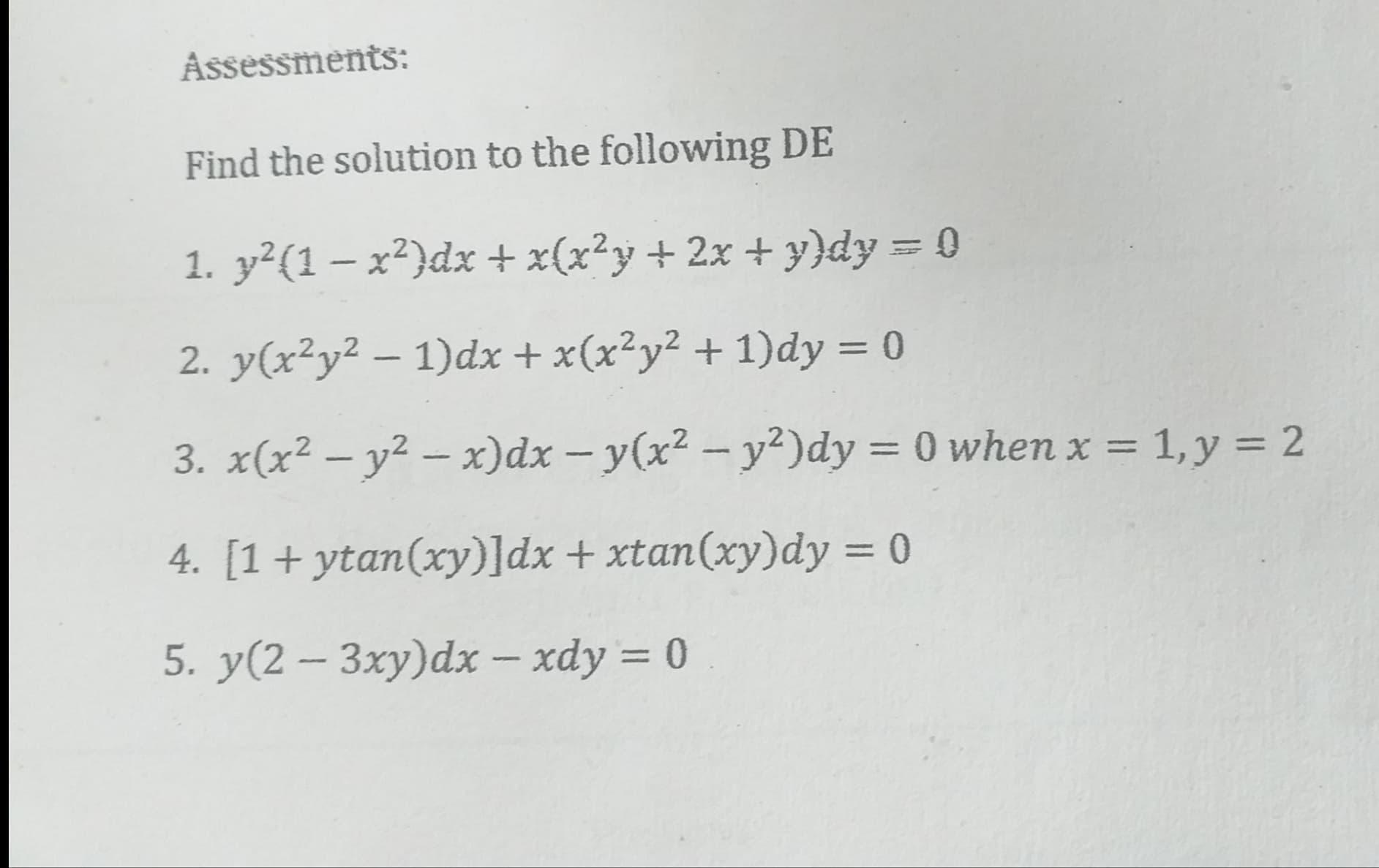 | 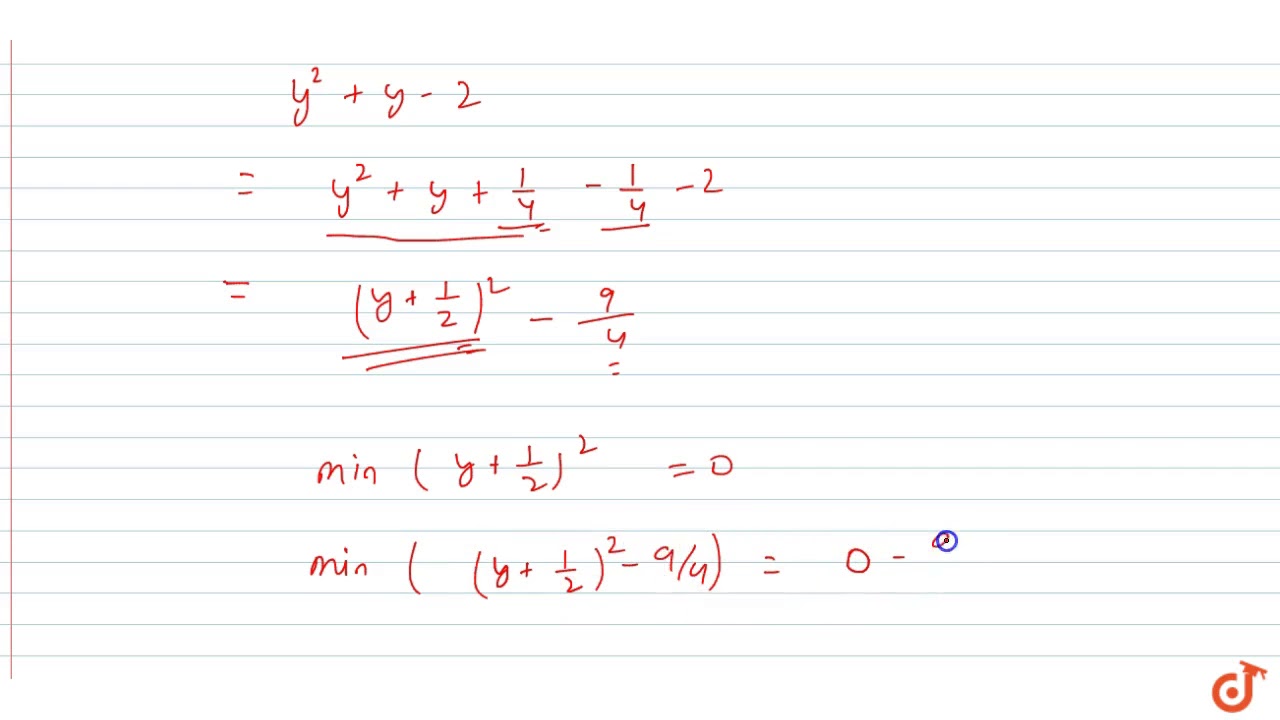 |
「(x^2+y^2-1)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
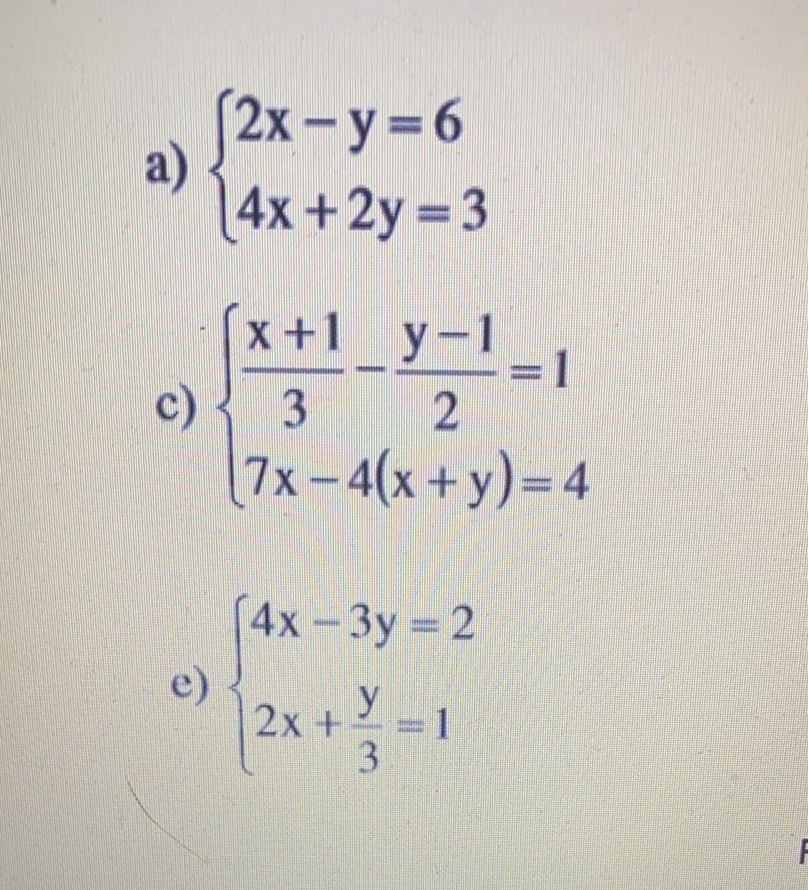 |  | 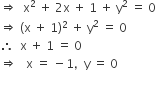 |
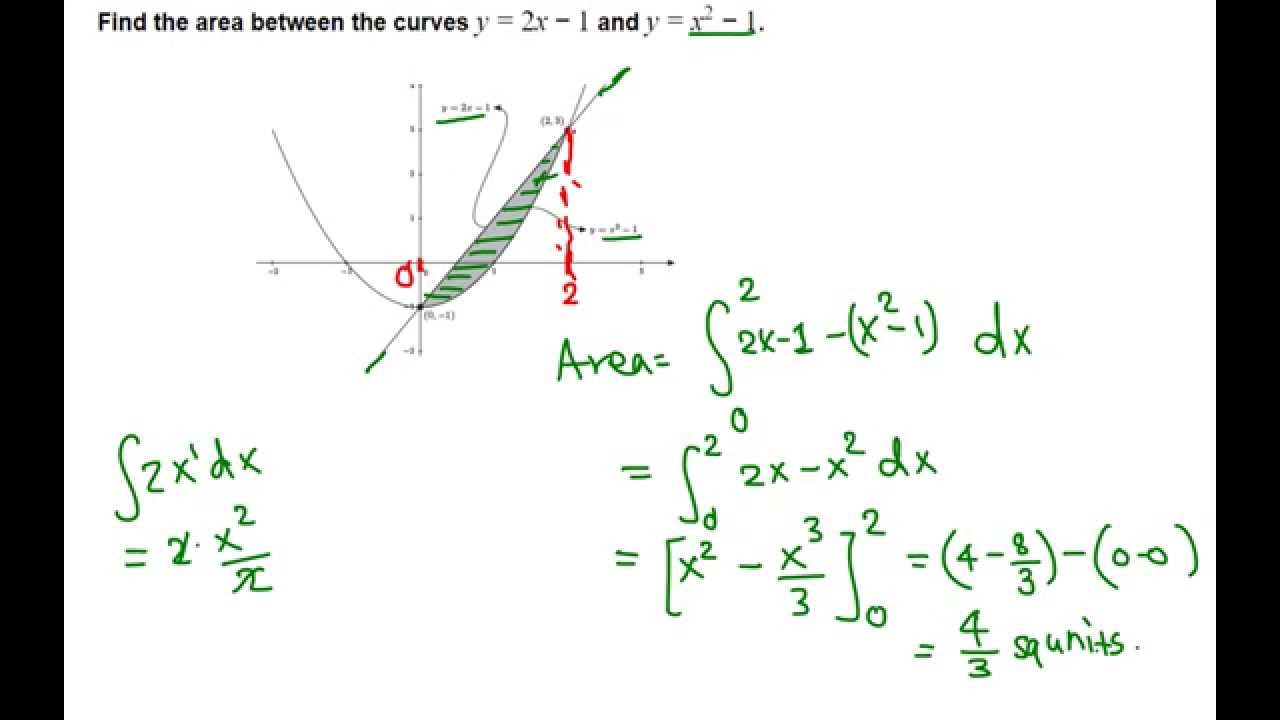
A 1 B 0 C 1 D 2 algebra; Step by step differentiation x2 y2 = (2x2 2y2 −x)2 2x 2y( dy dx) = 2(2x2 2y2 − x)(4x 4y( dy dx) −1) x y( dy dx) = (2x2 2y2 −x)(4x 4y( dy dx) −1)
Incoming Term: x^2-y^2+2x+1, x^2+y^2=1, x^2+y^2=1 graph, (x^2+y^2-1)^3, x^2+y^2=1 dy/dx, x ^ 2 + (y - 3 sqrt(2x)) ^ 2 = 1, (x^2+y^2+1)dx-2xydy=0, x ^ 4 - y ^ 2 + 2x ^ 2 + 1, (x+2)2=2x-1 standard form, x^2+y^2-1-2xy,



