まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半径をr、円周率をπ、求める球の体積をVとすると これが球の体積を求める公式です。 ※2つとも公式ですので覚えるようにしましょう。 公式を覚えたら次ページの練習問題にチャレンジ! 1ページへ戻る 前のページを読む 1/2 次のページを読む ・ 角柱と 球の体積 最後に、球の体積問題を解説します。 球の体積 \(V\) は $$ V= \frac{4}{3} \pi r^3 $$ という公式で求まります。 この公式がどうやって出てくるかを説明するには高校数学の積分が必要なんで、中学生はもう覚えてしまいましょう。の体積 V = Sh V = S h 体積 = 底面積 × 高さ 円柱の体積 半径 r、高さ h の 円柱 えんちゅう 円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。 円柱 えんちゅう の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 どうしゅつ 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の

球の体積 表面積 無料で使える中学学習プリント
球 円柱 共通部分 体積 重積分
球 円柱 共通部分 体積 重積分-球とは?体積・表面積の公式や求め方、証明(積分)と計算問題 動画の概要欄というものは文字通り動画の概要を説明すべきスペースであるはずだが、それをその通りに実現しているものは少ない気がする Sphere02 球の体積の公式をつかいましょう! 球の体積の公式は、4πr3 / 3でしたね。 4πr 3 / 3 にr=3を代入します。 4π×3 3 / 3 = 36π・・・(答) となります。 簡単ですよね? 球の体積の公式は必ず覚えましょう! 球の表面積に関する問題 下の図のように、半径3の半球があるとき、この球の表面積を求めよ。 解答&解説 半球(球を2等分したうちの片方)ということに注意しましょう!




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
球の体積の解説 球の体積は 4/3×円周率×半径×半径×半径=体積 で求めることができます。 円周率をπ、半径をr、体積をVとすると、 V=4/3πr 3 となります。 球の体積を求める公式 体積=4/3×円周率×半径×半径×半径 半径6cmの球の体積は何cm 3 ? ※円周率を314でおこなう場合 → 4/3×314×6×6×6 → cm 3 ※円周率をπでおこなう場合 → 4/3×π×6×6×6 → 864π 3 → 2πcm 3 単位が違う場合球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。 もくじ 球の体積を求める公式 球の体積を求める計算問題 半径から球の体積を求める問題 2種類の球の体積比を求 球の体積の公式とその覚え方・語呂合わせ 球の体積の公式 球の体積を求める公式は以下の通りです。 球の体積は半径rのとき、 \(\frac{4}{3}πr^3\) となります。 球の体積の証明のためには積分を利用する必要があり、少し難易度が高くなっています。
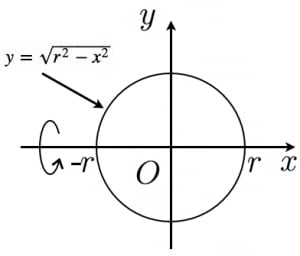
この記事の目的: 球体の体積 を求める式の意味を中学生にもわかるように説明する. 球の体積 体積 目標:上式で求まる理由を知る(積分等の高校数学を使わずに) はじめに;(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして 求める球体の半径は、三平方の定理で求められます。 また、体積は積分という方法を使って計算します。 どこまで勉強しているかは分からないのですが、 分からないときは補足で不明点を挙げて頂けると ポイントだけの説明ができるかも知れません。
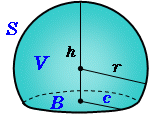
薄い球殻の体積を求めたい。 球殻は、中心を同じくする大きい球と小さい球とに挟まれた領域と言えるので、大きい球の半径を、小さい球の半径をとすると、体積は以下の式で表せる。 \begin{equation}V=\frac{4}{3}\pi (rdr)^3\frac{4}{3}\pi r^3\end{equation}球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集 = 0 とすることで球欠の体積公式: V=\dfrac {1} {6}\pi h (3r^2h^2) V = 61 πh(3r2 h2) が得られます。 球冠,球帯の表面積 高校数学の範囲外ですが,計算は体積より簡単です。 非常に美しい結果です。 球冠,球帯の表面積はその高さに比例する。 注:球帯の高さとは底面と天面の距離です。 球の体積と表面積の公式の覚え方・積分での求め方 の表面積の証明1とほぼ同じことをやるだ



1




中学数学 球の体積の何で 数樂管理人のブログ
球の体積 ボールの体積、表面積を求める。 とても分かりやすかった。 高精度計算サイト最高‼‼ 学校の宿題の自由課題で使わせていただきました。 漠然と、立方体の辺の長さが2倍になれば大きさが4倍になるのと同じように、球体も直径が2倍になれば 球の体積の求め方公式 半径 の球の体積を とすると、球の体積 は、次の公式で求められます。 (例題)半径5cmの球の体積を求めましょう。 求める球の体積を 、半径を とすると より 答え cm³ 球の表面積の求め方公式 半径 の球の表面積を とすると、球の表面積 は次の公式で求められます。 (例題)半径が4cmの球の表面積を求めましょう。 求める球の表面積を 、半径を とする2 球の表面積を出す公式での求め方 21 円柱の側面積と球の表面積の関係;



球の体積と球の表面積の公式 求め方 証明や計算問題も解説 受験辞典



数学 球の表面積を積分で計算してもうまくいかない人へ
四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 体積の求め方、覚え方 体積の公式の覚え方は簡単です。球の体積を除けば、たった2つの公式を覚えるだけで済むからです。球の体積は、中心から表面までの距離(常に一定)を半径rとすると、 4/3 * π * r 3 であらわされます。πは、円周率のことです。円周率は と続きます。実際の計算では、314などのように近似値で行うことがあります。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、 4 × 円周率 × 半径 × 半径 ってわけだね。 たとえば、半径30cm のサッカーボールがあったとしよう。 このボールの皮の面積、つまり表面積は、 4 × π × 30 × 30 = 3600π cm^2 になるんだ。 公式にいれて計算するだけでいいんだ。 チョー便利な公式じゃない? 笑 ただ、球の表面積には、 チョー覚えにくい っていう欠




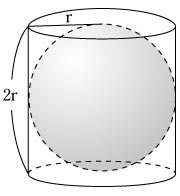
تويتر はりねずみ على تويتر ちなみにこれがなんで成り立つのか最後までよくわからなかった 結果的にそうなるだけなの カバリエリの原理みたいに普遍的な原理があるの 一方で球 の表面積が円柱の表面積の2 3倍ってのもなかなかきれいなんだけど 体積と同じ2 3倍




球の体積と表面積 数学i フリー教材開発コミュニティ Ftext
球の体積の公式は(4πr 3)/3で、こちらもやはりr 3 のところに、立方体何個ぶんかということが現れてきています。 中学では新しく扇型の面積や中心角の求め方を習いますが、これは円を元にして考えることができます。V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin球の体積は \(\dfrac{4}{3}{\pi}r^{3}\) となります。 語呂合わせとして有名なのが、 「身の上に心配あるので参上」 です。 分母の3の上に分子の4があることを「身(3)の上に心(4)~」という言葉で表しており、とても上手い語呂合わせとなっています。 「心配ある」という部分は表面積の公式と




球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
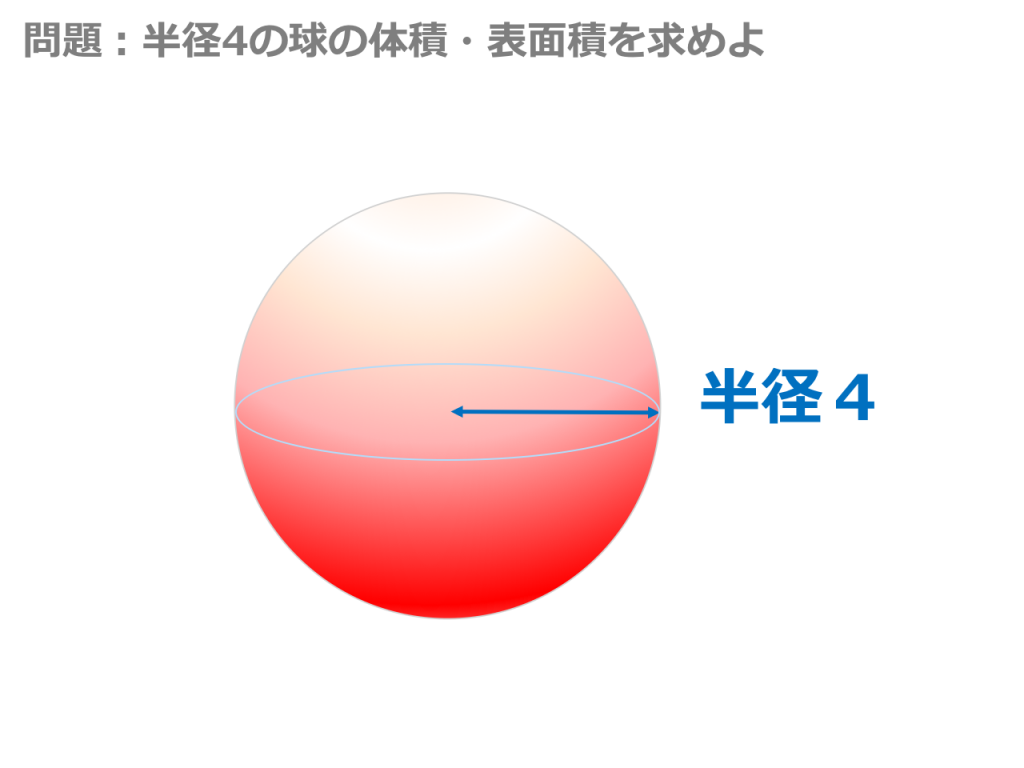
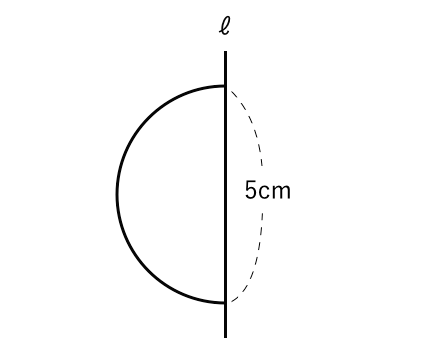
それでは、問題を通して球の公式をしっかりと身につけていきましょう! 半径6㎝の球の体積、表面積をそれぞれ求めなさい。 解説&答えはこちら 答え 体積: 表面積: 体積 表面積 次の図形の体積、表面積をそれぞれ求めなさい。 解説&答えはこちら 半径が3㎝だから、 ということで体積の公式に代入しましょう。 引用東京新聞 答えはこちら 半径2㎝の半円を1回転させると、半径2㎝の球ができあがります。 引用東京新聞 答えはこちら 半径3㎝の球の体積を求めると 円柱の高さを として 球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.



3




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
もくじ 1 球の体積を出す公式での求め方 11 円柱と球の体積の関係;球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめてい



至急 球を4等分したものの体積の求め方を教えてください Yahoo 知恵袋



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス
球の表面積: 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に心配アール三乗」 意味はわからないかもしれませんが,何度も口に出していると自然と覚えます。 球体の表面積や体積を求めるときは,今でも語呂で公式を思い出しています。 円の面積の公式: \pi r^2 πr2 等と混同しないよう正しく覚えましょう。 球の体積と表面積の公式を用い分かり易い体積から求めておきます。 半径 の球の体積は なので 半球 の体積は くり抜く直方体の体積は よって求める体積 は 体積や面積を求めるとき、 公式が通用しないとき は 『 部分 』+『 部分 』 『 全体 』-『 部分 』 を利用することはよくあります。 これはその典型です。 表面積は簡単には求まりませんが、部分部分は難しくはありません。 まずは半球の表面部分、 展開図は書けないけど球球の表面積体積公式 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから, S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π, 答え 12π cm², ~立体の体積・表面積を求める公式まとめ~, 立方体・直方体の体積の求め方, 円柱の体積




球に関する公式 理数系学習サイト Kori




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張
解答 1 基本計算モードを選択。 2 球の体積の式4π× () 3 /3を入力。 3 答えを求める。 これより地球の体積は約x10 12 立方kmであることがわかる 球の体積の計算機半径→体積、体積→半径 球の体積 球の体積を計算します。 球の体積は、rを半径とすると、 球の体積 = 4/3 ×π× r 3 で表されます。 球の体積の求め方 円の面積は π×r 2 であり ある高さ「x」で球を切り取った時の面積は π×( r x ) 2




この答えは2p になるんですが この球の体積の求め方とどうやったらこの答 Clearnote



球の表面積の公式の求め方




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の表面積の求め方 公式と計算例



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



3
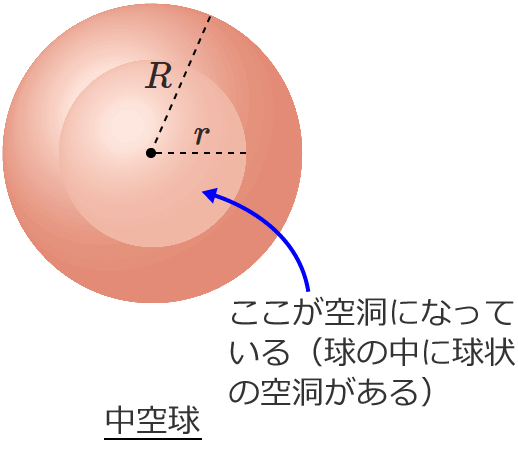



立体の体積を求める公式




球表面積 なぜ 勉強しよう數學 Ptnoe



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



Lh3 Googleusercontent Com Proxy 6ombezg0q Fbykxeramwkegvax2ixv9l1racg6bxkqmq27sllfb2gf Sjxp5uxgymciwzfvrihie7z5rbsxpa0dds15vvnrcvmvppke0s8yfmb5xzdn6iqnj7c7c4izvtrr Zh1uyu3mbp80fjmctuekhme05 Rtlm98pdmuipmhlukzhxk3zmdwxusmgdicygzx1u7kqalu Ytjqkiihnejynhpappfp2iptpq8pkjoe3zxd4a3indmymvssayw1mcqxg4zctabqyrkiecse2ga4 P6zndlcunj4hkzm7ulwgvzqccxofp9zf8gao9jyhztyksvcitbpj4pp6ixfval54 Vmawuzhmhhsufa6gowmgydsjsfmcshqqy



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




Mathematics 球の体積と表面積を求める公式 働きアリ
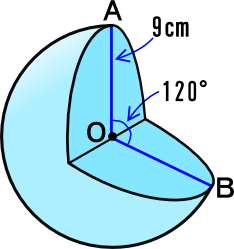



中学1年数学練習問題 球の体積と表面積の求め方と解答 空間図形
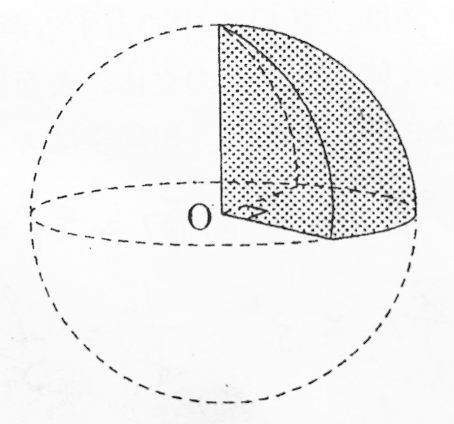



球の問題 苦手な数学を簡単に




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の表面積の求め方 その3 感じる科学 味わう数学



球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba



球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba
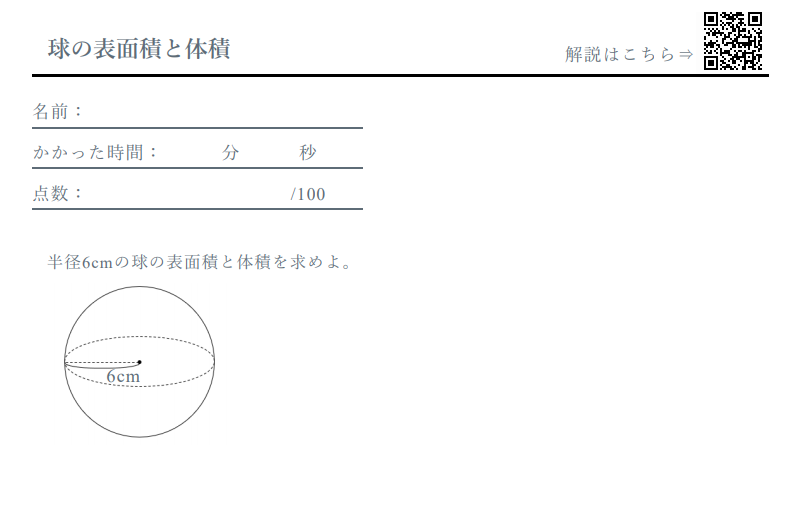



球の表面積と体積 計算ドリル 問題集 数学fun




中1数学 空間図形 球の体積の求め方 Youtube



3




球の体積 表面積 無料で使える中学学習プリント



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



研究




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



球の体積と玉率 雑学のソムリエ
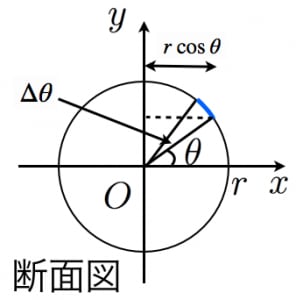



球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語



球の体積 計算が簡単にできる電卓サイト




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト
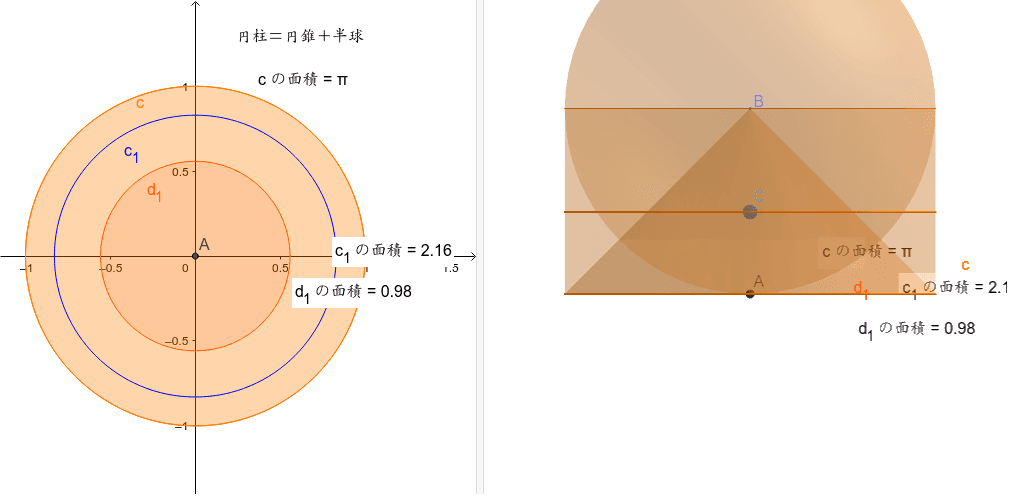



球の体積の求め方 Geogebra



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




曲面 番外編 曲面の面積 身勝手な主張



回転体 球について 苦手な数学を簡単に




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




角錐 円錐の体積と表面積の公式 数学fun




球表面積體積覚え方 球の表面積と體積の公式の覚え方 Tfdvy




球の表面積の公式について みたにっき はてな



球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語



一部が欠けた球の体積 高精度計算サイト



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




中1数学 球 練習編 映像授業のtry It トライイット
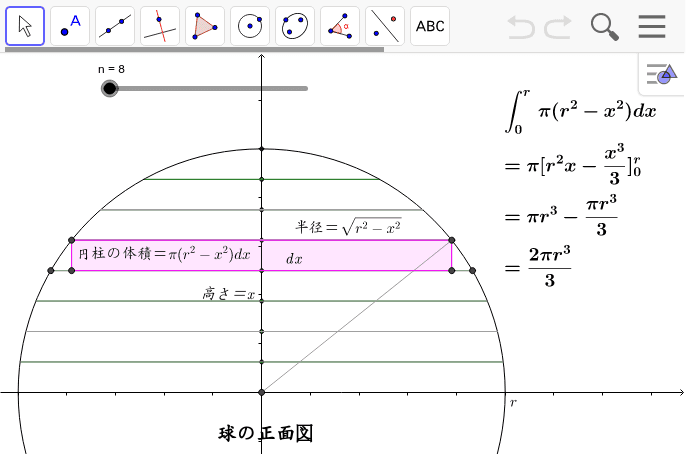



球の体積の積分 Geogebra




半球の体積と表面積を計算する 具体例で学ぶ数学




円柱の水槽に球を入れる問題 苦手な数学を簡単に




中1 中1数学 球の体積と表面積 中学生 数学のノート Clearnote
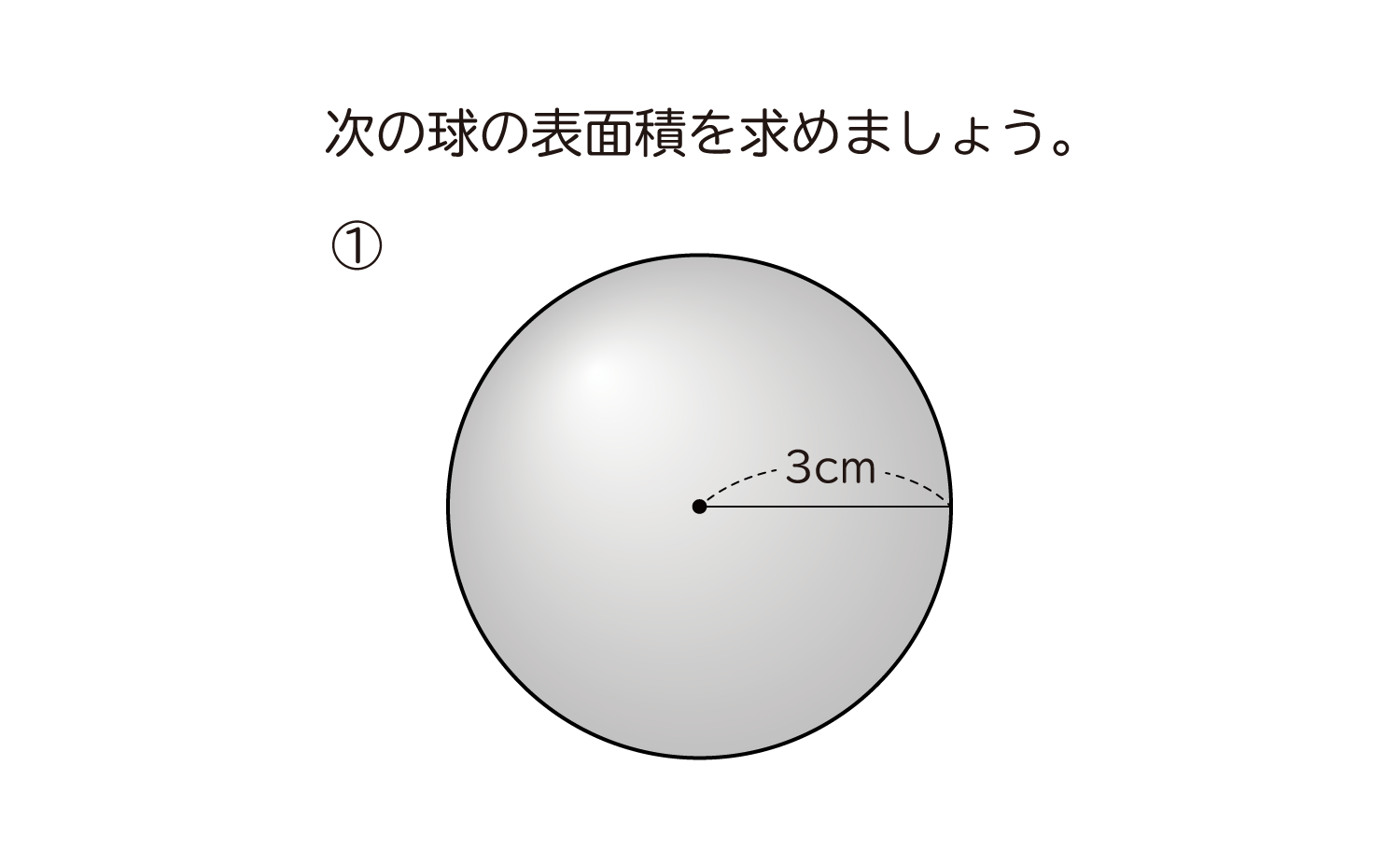



中学1年生 数学 無料問題集 球の表面積 おかわりドリル




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ




球表面積證明 球の體積と表面積 Dykpo




数学講師必見 中学数学でも必須 球の体積 表面積の覚え方と導出まとめ 高校数学 塾講師ステーション情報局




球の表面積の公式と球の体積の公式 中学生の数学 要点 Yattoke 小 中学生の学習サイト




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




球の体積の求め方 感じる科学 味わう数学




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ




球の体積 球の表面積の公式の導出 積分 優技録
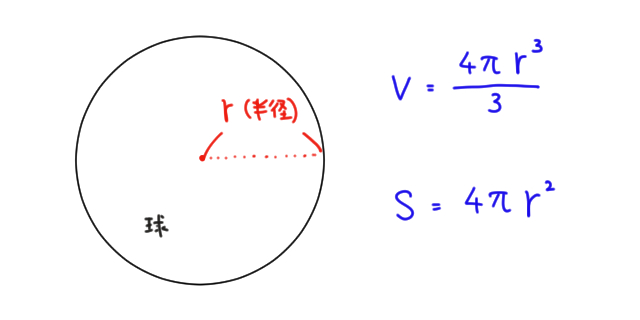



球の体積と表面積 公式と計算問題と証明 Irohabook




球の表面積 体積 身勝手な主張
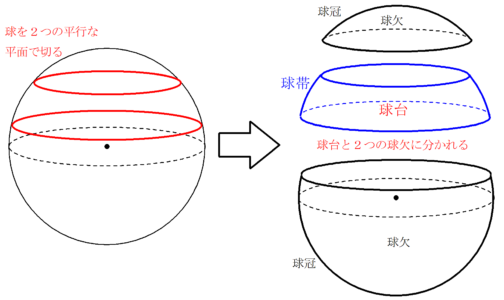



球台と球帯 Fukusukeの数学めも




球の体積と表面積 Youtube



球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
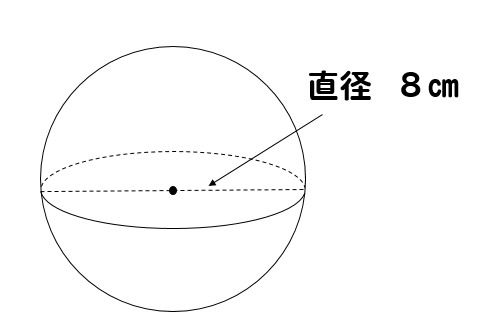



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の表面積と体積の公式 数学fun




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
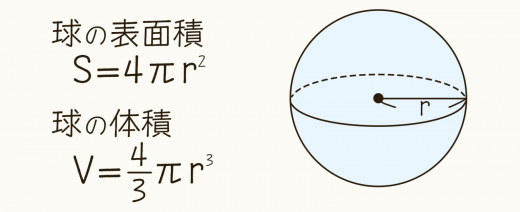



球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語




球の体積の求め方を教えていただけませんか よろしくお願いしますm M Clearnote




球の体積の公式 求め方や覚え方のコツを紹介するよ 中学や高校の数学の計算問題




球の体積と表面積の求め方 公式を使う中学数学での計算 Hatsudy 数学 科学




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
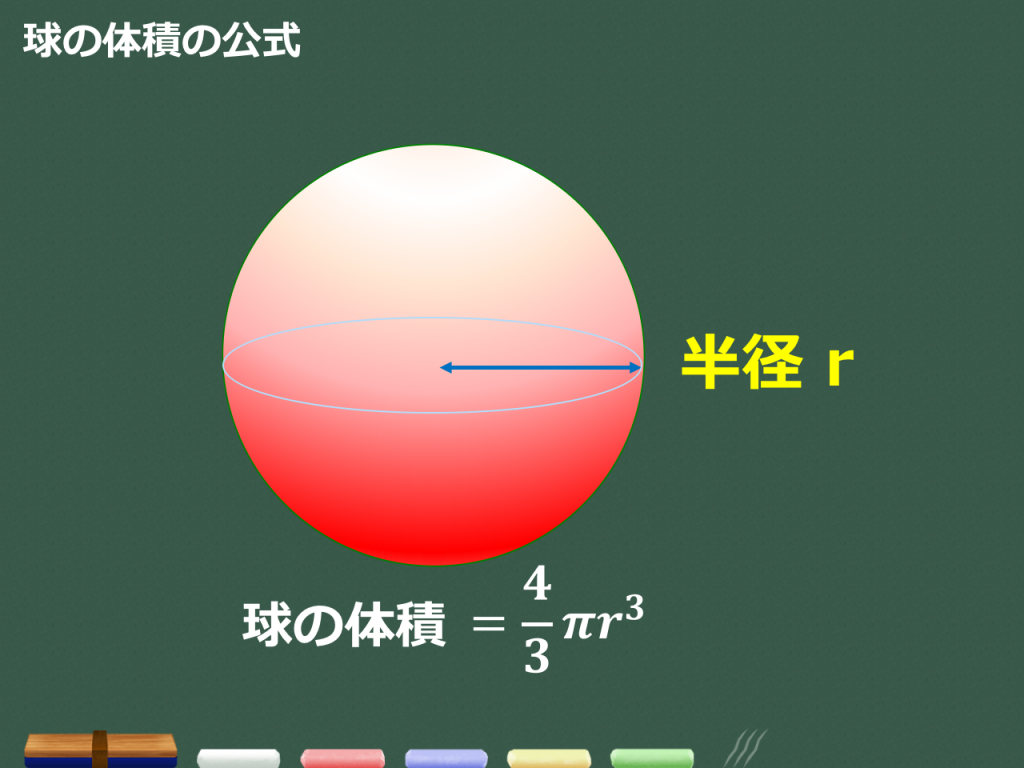



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



大学入試問題



Studydoctor球の表面積や体積の公式と求め方 中学1年数学 Studydoctor
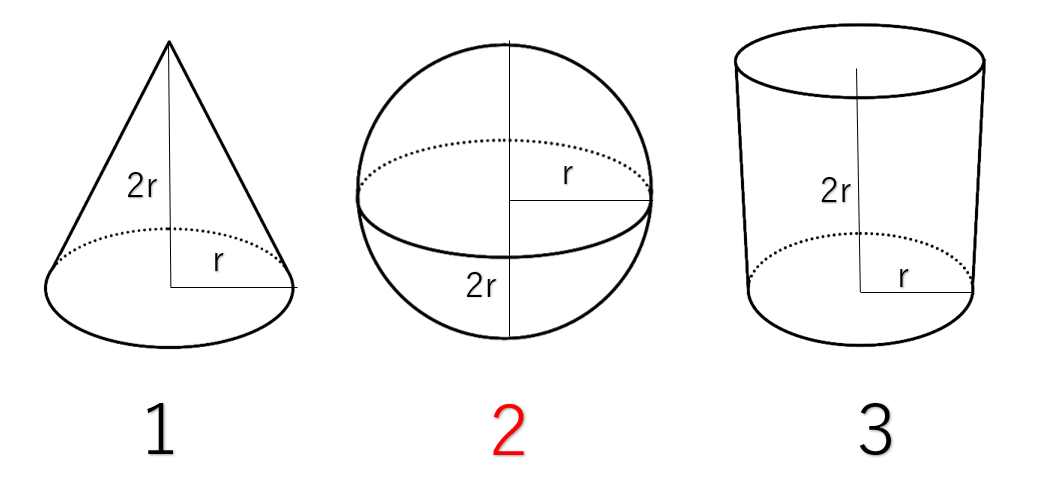



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾




球体の体積 中学生に分かるように真剣に考えてみた うちーノート




中1 数学 6 5 球の体積 表面積 Youtube




球の体積公式の微分が表面積になっている理由 Youtube



数学トピックq A




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




積分球公式球的體積 Jvvx




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




球の表面積と体積の求め方 苦手な数学を簡単に




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ



球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




中1 数学 中1 84 球について Youtube




球の体積 球の表面積の公式の導出 積分 優技録


