Graph of xy=4 Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving process If it's not what You are looking for, type in into the box below your own function and let us find the graph of it The graph of xy=4 represents a graph of a linearF(2)=3 means that when you substitute x=2 in the equation y = f(x) like this y = f(2) That the value of y is 3 because f(2) = 3 That means that the graph contains the point (x,y) = (2,3) So we plot that point (2,3) and the line x=3, which is a vertical line through 3 on the x axis, the green line below We want to reflect that point acrossSelect a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Substitute the x x value 2 2 into f ( x) = √ − x 4 f ( x) = x 4 In this case, the point is ( 2, ) ( 2, )
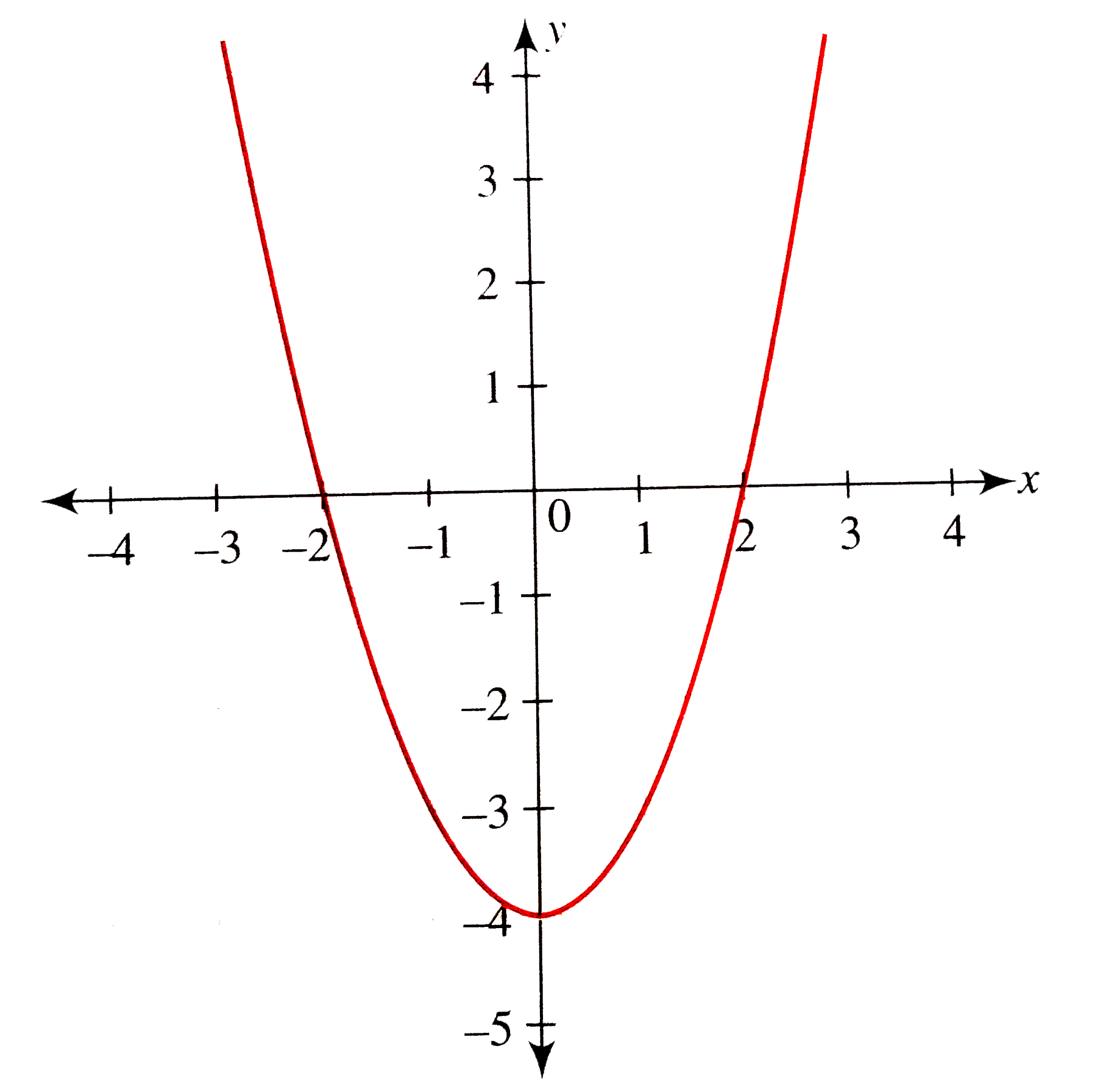
Quadratic Functions
Y f x 4 graphed
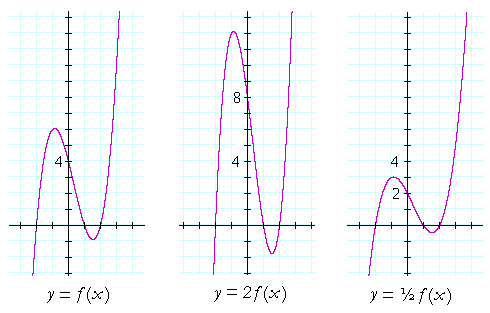
Y f x 4 graphed-Transcribed image text Consider the function f (x) with graph shown below y=f(x) 10 6 АМА 4 2 2 C x Approximate Alºf (x), ie the area under the curve from x=0 to x=10 (a) Using ten rectangles and left endpoints (b) Using Ax = 2 and right endpointsFor example, (3, 2) is on the graph of f (x), (3, 4) is on the graph of 2f (x), and (3, 1) is on the graph of f (x) Graphs of f (x), 2f (x), and f (x) To stretch or shrink the graph in the x direction, divide or multiply the input by a constant As in translating, when we change the input, the function changes to compensate
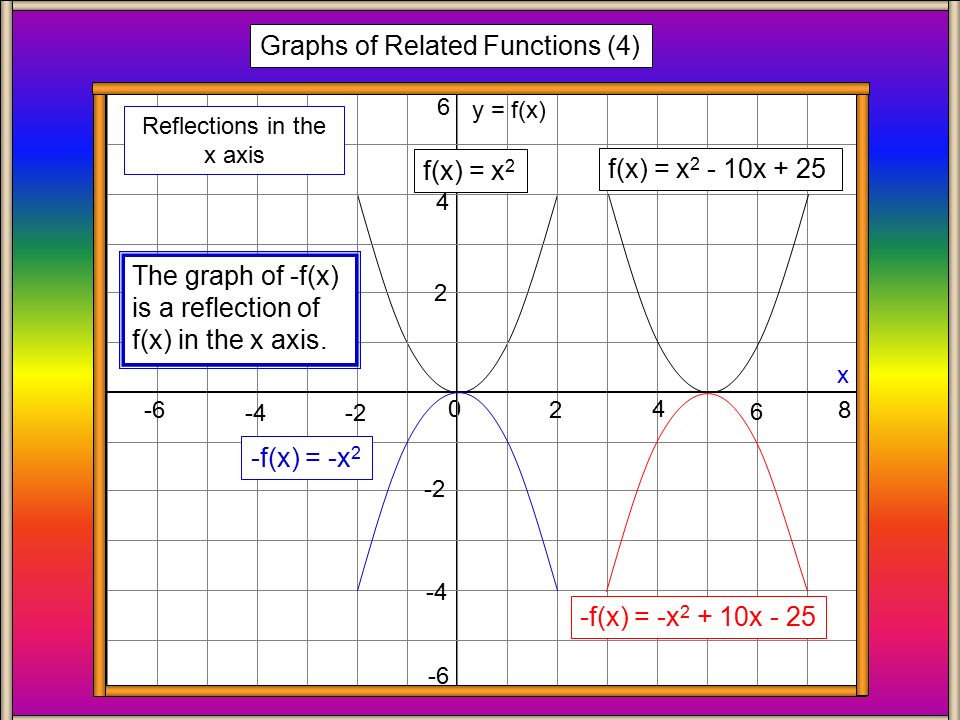



F X A X Y F X Graphs Of Related Functions 1 F X X 2 F X 2 X F X 5 X Vertical Translations Ppt Download
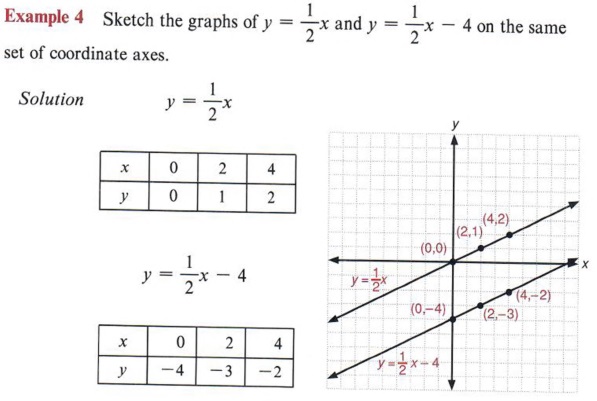
So00 бооо 00 "10 6 4 2 2 6 10 00 "4000 6000 8o00 as x → 00, y → ∞ and as x → ∞, y→ ∞ as x → 00, y → ∞ and as x → ∞, y →→ ∞ O as x → o∞, y → ∞ and as x → ∞, y → 00Changing "c" only changes the vertical position of the graph, not it's shape The parabola y = x 2 2 is raised two units above the graph y = x 2 Similarly, the graph of y = x 2 3 is 3 units below the graph of y = x 2 The constant term "c" has the same effect for any value of a and b Parabolas in the vertexform or the ahk form, y = a(xWe will use 1 and 4 for x If x = 1, y = 2(1) 6 = 4 if x = 4, y = 2(4) 6 = 2 Thus, two solutions of the equation are (1, 4) and (4, 2) Next, we graph these ordered pairs and draw a straight line through the points as shown in the figure We use arrowheads to show that the line extends infinitely far in both directions
The graph of y = f (x) is shown 5 4 3 2 1 1 2 4 5 Determine the sign of the following limits, if they exist f (3 h) – f (3) is lim h→0 h Positive 3 it Who are the experts?You can clickanddrag to move the graph around If you just clickandrelease (without moving), then the spot you clicked on will be the new center To reset the zoom to the original click on the Reset button Using "a" Values There is a slider with "a =" on it You can use "a" in your formula and then use the slider to change the value of "aView my channel http//wwwyoutubecom/jayates79
Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Substitute the x x value − 3 3 into f ( x) = √ x 4 f ( x) = x 4 In this case, the point is ( − 3, 1) ( 3, 1) Tap for more steps The graph of y = f(x) is graphed below What is the end behavior of f (x)?It's a double root for y^2, but not y on its own Think about y=xc, that's a single root Similarly the graph of y^2=(xc)^2 will cut through the x axis rather than just touching it y=(xd)^2 will be a double root, just touching the x axis Square it to get y^2=(xd)^4 will give you the same 'just touching' effect of a double root



Fze0qxgxb Rwum
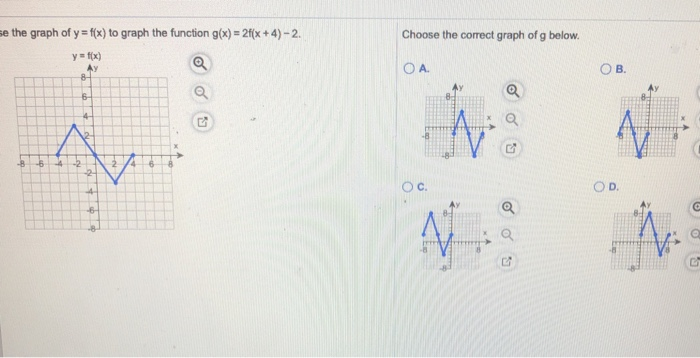



Solved Se The Graph Of Y F X To Graph The Function Chegg Com
#7 Prim3 12 0 In a graphing calculator, you should graph this cristo y = f (x) 4 and you will get a straight line 4 units down It's going to be Suppose (4,2) is a point on the graph y=f(x) What is a point that would be on the graph if y=10f(x)5Precalculus questions and answers The graph of y = f (x) is shown below (dashed curve) Manipulate the green draggable points to obtain the graph of y= f (x – 4) – 2 (solid curve) Note if you need to flip the solid curve, just drag one of the moveable points down into the lower quadrants of the graph 7 1 1 6 5 4 3 1 2 1 1C9 8 7 6 5 4 3 2 2 3 4 5 6 0 1 (4 2 3 5 6 7




The Graph Of Y F X The Derivative Of F X Is Shown Below List The Intervals Where The Graph Of F Is Concave Down 4 2 U 2 4 2 2 4 0 0 4 Study Com



Solved Question The Graph Of Y F X Is Shown Below Dashed Curve Reposition The Two Green Draggable Points To Obtain The Graph Of Y F X 4 Course Hero
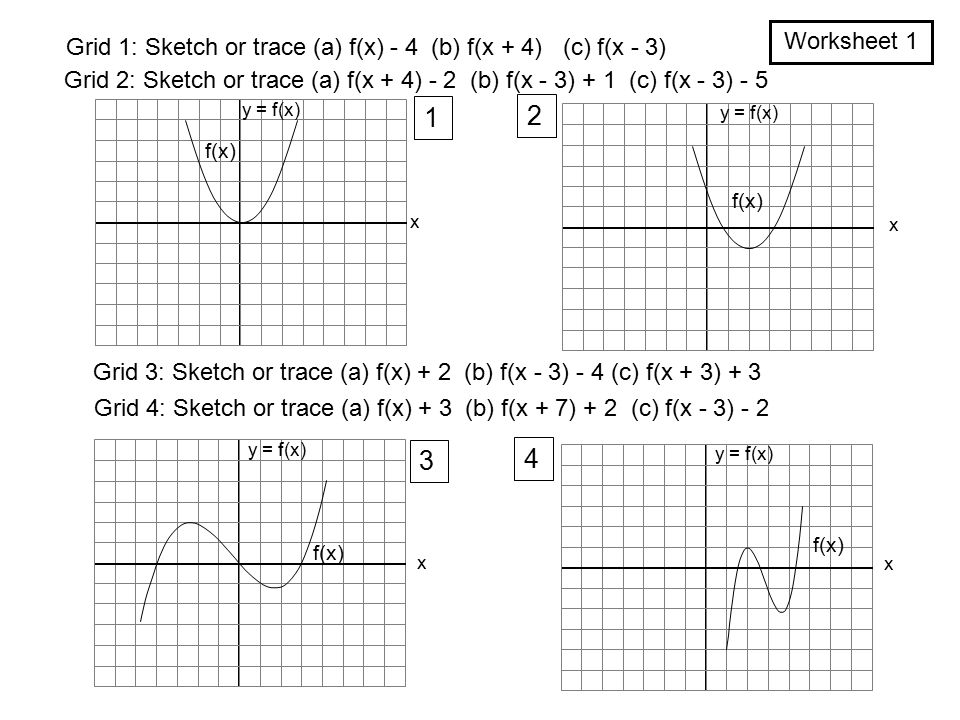
2 123 Multiple choice 4 For the graph > O for A x > C B 01 5 For the graph at < O for A 6 For the graph at fight, the value of x at which the rate of change of y with respect to x is aqual to 2 is A 1=1 1 E None of the 7 The turning p3ints on the graph of y shown at fight occur A only at x = 0 B when 2 and 2 c when 1=4, O and 4 DSimple transformation for y=f(x) functionGraph the parent quadratic (y = x^2) by creating a table of values using select x values The graph of this parent quadratic is called a parabolaNOTE Any



Graphing Quadratic Functions
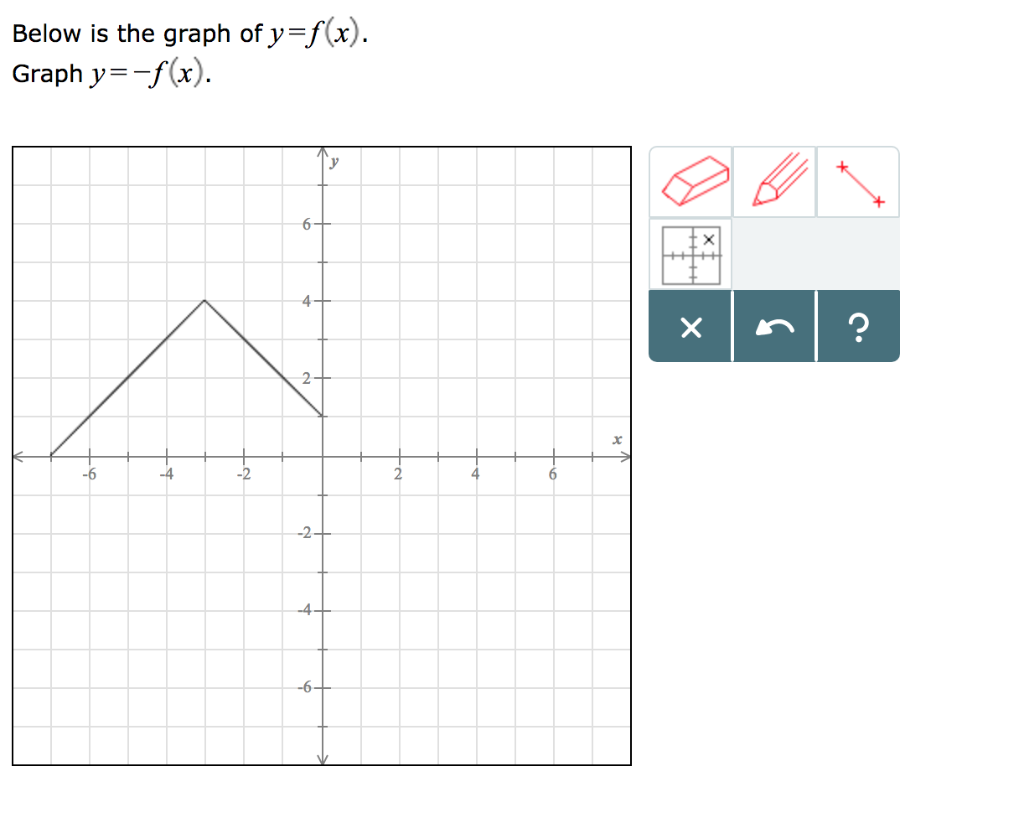



Solved Below Is The Graph Of Y F X Graph Y F X 4 6 4 Chegg Com
The graph of the function y = f(x) consists of all of those ordered pairs of numbers (x,y) that satisfy y = f(x) 2 The ycoordinate of a point on the graph of the derivative of a function tells you the slope on the graph of the function at the corresponding x 3 The first derivative and local extrema See the explanantion This is the equation of a circle with its centre at the origin Think of the axis as the sides of a triangle with the Hypotenuse being the line from the centre to the point on the circle By using Pythagoras you would end up with the equation given where the 4 is in fact r^2 To obtain the plot points manipulate the equation as below Given" "x^2y^2=r^2" ">"Compared to the graph of \(y = x^2\text{,}\) the graph of \(f (x) = 2x^2\) is expanded, or stretched, vertically by a factor of \(2\text{}\) The \(y\)coordinate of each point on the graph has been doubled, as you can see in the table of values, so each point on the graph of \(f\) is twice as far from the \(x\)axis as its counterpart on the basic graph \(y = x^2\text{}\)




Choose The Correct Graph Of G Below Graph Of Yf X To Graph The Function X Homeworklib
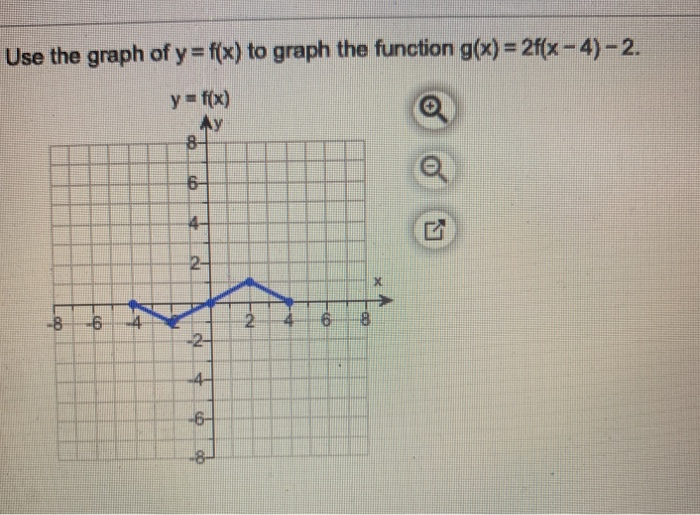



Solved Use The Graph Of Y F X To Graph The Function G X Chegg Com
Here, f(x) = x 2 and g(y) = 8 4y And so, x 2 = 8 4y or x = 10 4y, for x2 >= 0 x 2= 4y 8 or x = 4y 6, for x 2Graph of z = f(x,y) New Resources Creating Distances in 3 Space;100% (2 ratings) a) For y = 15 f(x), the graph will stretch along Yaxis by 15 times to get the graph as shown Note that the height of lines parallel to Xaxis has increased from 1 to 15 now View the full answer




Ch 1 Graphs Y Axis Quadrant Ii Quadrant
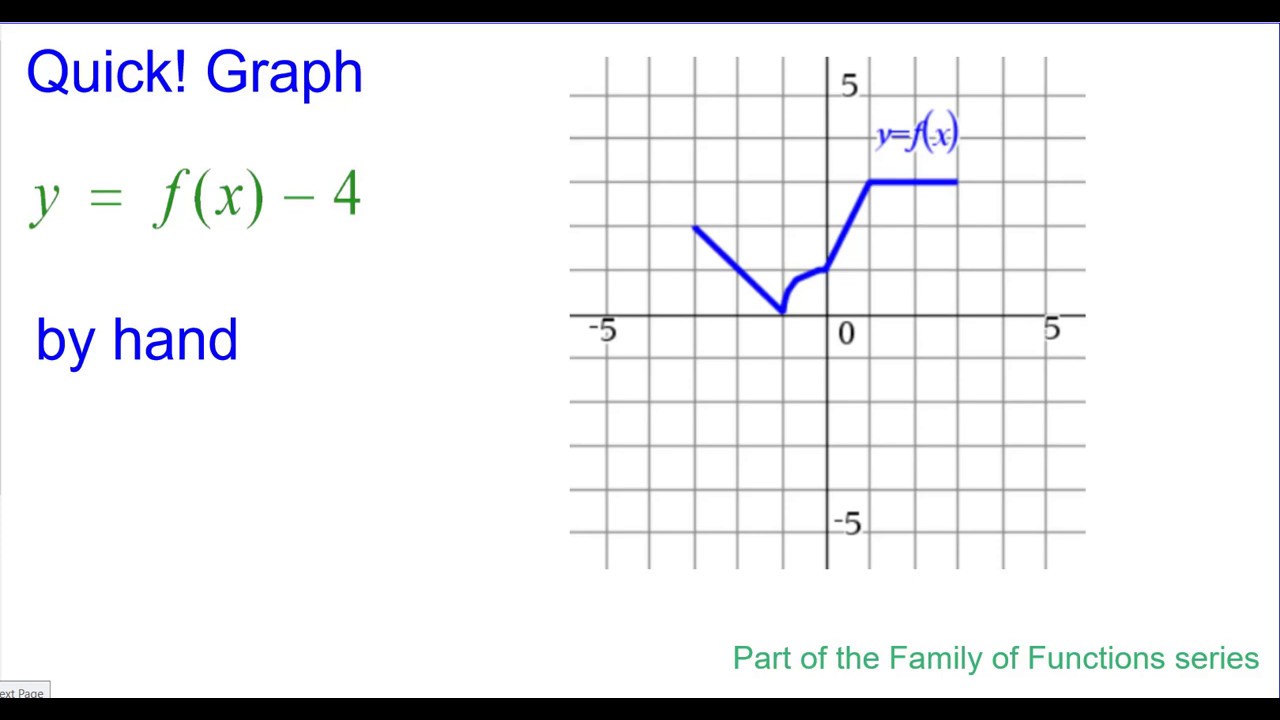



Quick Graph Y F X 4 Youtube
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicThe graph of y = f (x) is the graph of y = f (x) reflected about the yaxis Here is a picture of the graph of g(x) =(05x)31 It is obtained from the graph of f(x) = 05x31 by reflecting it in the yaxis Summary of Transformations To graph Draw the graph of f and Changes in the equation of y = f(x) Vertical Shifts y = f (x) c A general straight line has the following form as a function y = f(x) = axb where a is the slope of the line and b the intercept with the y axis Now your function has the form f(x) = 0x 4 It has slope a = 0 so it never changes (a constant) and intercepts the y axis in 4 and remember NEVER CHANGES!!!



Rhay Weebly Com
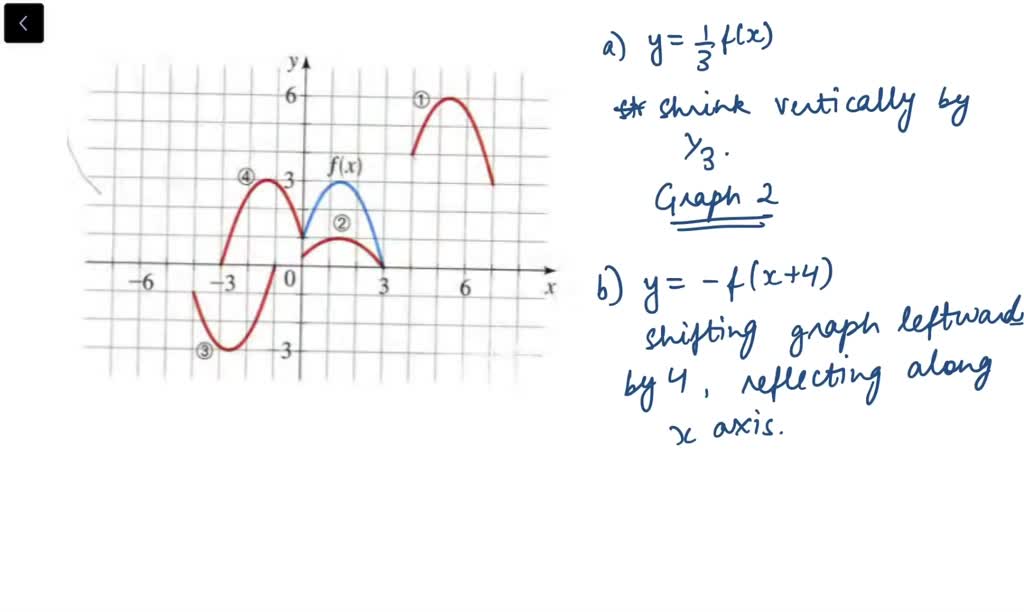



Solved The Graph Of Y F X Is Given Match Each Equation With Its Graph A Y Frac 1 3 F X B Y F X 4 C Y F X 4 3 D Y F X
Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and images (Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality highGraph f (x)= (x4)^2 f (x) = (x − 4)2 f ( x) = ( x 4) 2 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 1 a = 1 h = 4 h = 4 k = 0 k = 0
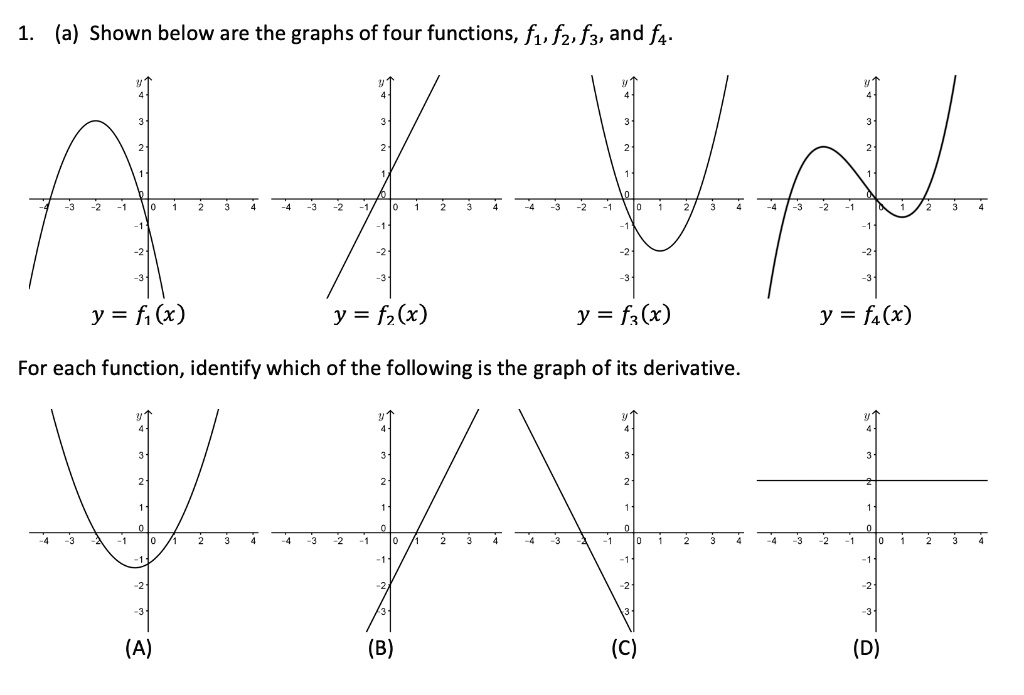



Solved A Shown Below Are The Graphs Of Four Functions F1 Fz F3 And F4 Y X Y Fz X Y Fz X Y F X For Each Function Identify Which
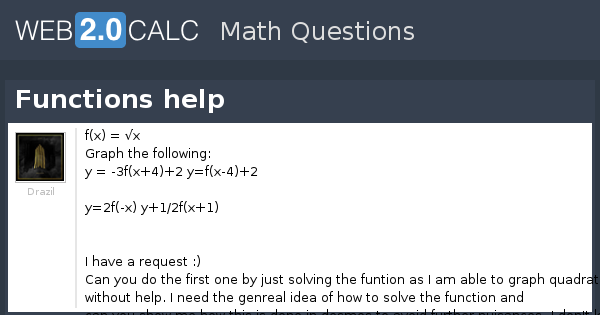



View Question Functions Help
A surface in space can be defined by a function such as z = f(x,y) z = f ( x, y) defining coordinates (x,y,z) ( x, y, z) on the surface so that a graph can be plotted in a rectangular coordinateSo, you can build your graph giving values of x say, 1, 2, 3,and y willSubsectionVertical Shifts Figure232 shows the graphs of f(x)= x24, f ( x) = x 2 4, g(x)=x2−4, g ( x) = x 2 − 4, and the basic parabola, y = x2 y = x 2 By comparing tables of values, we can see exactly how the graphs of f f and g g are related to the basic parabola




If The Graph Of The Function Y F X Is Symmetrical About The Line X 2 Then Youtube



Y 2f X
Mathematics Instructional Plan – Algebra II Virginia Department of Education ©18 4 Have students graph Y 1 = f(x) = 2x 3 and its inverse, Y 2 = f −1(x) = 1 2 (x − 3), with Y3 = x Point out the symmetry of the graphs with respect to y = x Show several examples of finding the inverse both algebraically and graphically usingOpen Middle Pythagorean Theorem (2)C < 0 moves it down



Understanding Inverse Functions Studypug




Consider The Graph Of Y F X As Shown In The Following Figure Img Src D10lpgp6xz60nq Cloudfront Net Physics Images Cen Gra C01 E01 002 Q01 Png Width 80 I Find The Sum Of The Roots Of The Equation F X 0 Ii Find
Algebra Graph f (x)=2 f (x) = 2 f ( x) = 2 Rewrite the function as an equation y = 2 y = 2 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b• Beginning with the graph f(x)=x2, we can use the chart on the previous page to draw the graphs of f(x 2),f(x 2), f(2x), f(1 2x), and f(x) We could alternatively write these functions as (x 2)2,(x 2)2, (2x) 2,(x 2) ,and(x) The graphs of these functions are drawn on the next pageIf the graph of y = f (x) is translated a units horizontally and b units vertically, then the equation of the translated graph is y − b = f(x − a) For in a translation, every point on the graph moves in the same manner Let (x 1, y 1), then, be the coördinates of any point on the graph of y




Draw The Graph Of The Function Y F X 2 X Between X 1 2 And X 4
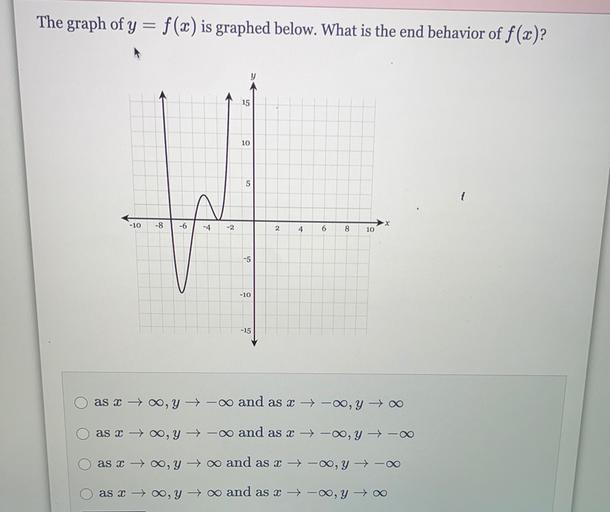



The Graph Of Y F X Is Graphed Below What Is The End Math
The graph of y = (2 x) 2 y = (2 x) 2 is a horizontal compression of the graph of the function y = x 2 y = x 2 by a factor of 1 2 1 2 Horizontal Stretches and Compressions Given a function f ( x ) , f ( x ) , a new function g ( x ) = f ( b x ) , g ( x ) = f ( b x ) , where b b is a constant, is a horizontal stretch or horizontal compression ofRemember f(x) reflects the graph to the right of theLet us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;
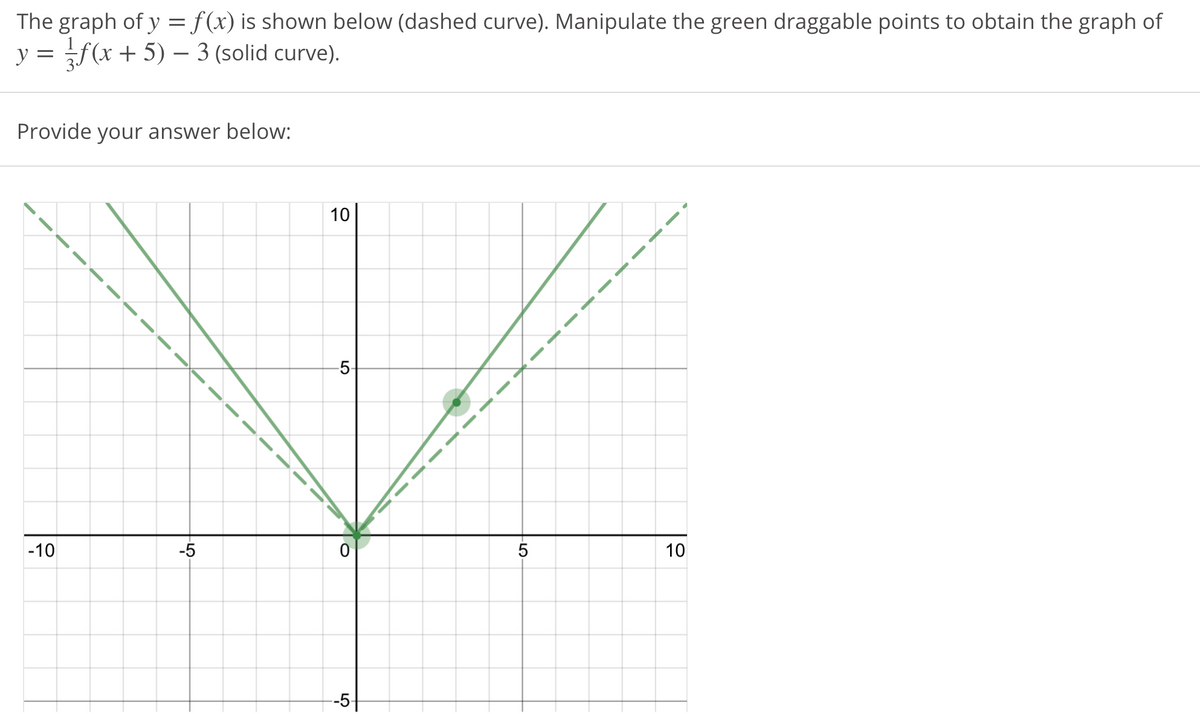



Answered The Graph Of Y F X Is Shown Below Bartleby
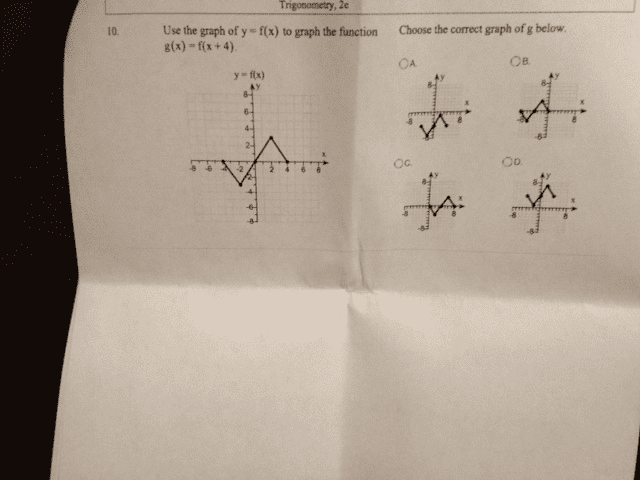



Oneclass Use The Graph Of Y F X To Graph The Function G X F X 4 Choose The Correct Graph
This is the graph of y = f(x) First I want to label the coordinates of some points on the graph Since, for each point on the graph, the x and y coordinates are related by y = f(x), I can put the coordinates of these points in a list x y = f(x)4 1 1 1 2 0 31By $f(x) = x^2 4$ I am telling you that if you input a number $x$ to this function then the function squares $x,$ subtracts 4 and returns the result Thus for example if $x = 3$ then $y = f(3) = 3^2 4 = 9 4 = 5$ To graph this function I would start by choosing some values of $x$ and since I get to choose I would select values that make the arithmetic easy For example $x = 0, x = 1, x = 1$Example Use transformations to graph f(x) = 3x 2 Start with a basic function and use one transformation at a time Show all intermediate graphs This function is obtained from the graph of y = 3x by first reflecting it about yaxis (obtaining y =




Intro To Combining Functions Article Khan Academy




Atlantic Canada Mathematics Curriculum Course 1 Y Level Teacher S Pilot Draft Guidelines Education Library Curriculum Guides Memorial University Dai
Answer (1 of 14) y=f(x) denotes any given function y=f(x) therefore denotes the negative of the function, the negative of the entire f(x) As such, it would look more like (f(x)) if you wanted it to be more clear, the exact same as writing y=f(x) You can see clearly that the negative is atMultiplying the values in the domain by −1 before applying the function, f (− x), reflects the graph about the yaxis When applying multiple transformations, apply reflections first Multiplying a function by a constant other than 1, a ⋅ f (x), produces a dilation If the constant is a positive number greater than 1, the graph willTranscribed image text 2 For each graph shown, determine where f(x) = 0 Express your answers using interval notation a) any y=f(x) b) 56 81% 42 6 28 14 2 ly=f(x) 64 2 4 2 2 4 INEL 2




Draw The Graph Of The Function Y F X 4 X Between X 1 2 And X 4




The Graph Of Y F X Is Given Above For What Value Of X Is Y F X 4 Undefined Brainly Com
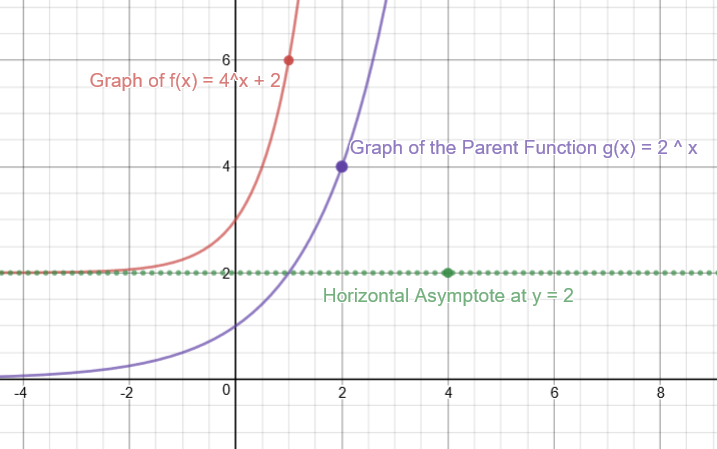
Steps to graph x^2 y^2 = 4Clearly not the straight line y=4!Algebra Graph y=4*2^x y = 4 ⋅ 2x y = 4 ⋅ 2 x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0



F X A X Y F X Graphs Of Related Functions 1 F X X 2 F X 2 X F X 5 X Vertical Translations Ppt Download




5 3 Inverse Functions Mathematics Libretexts
To draw the graph of f ( x) = x 4 x − 4 , you can first rewrite it as f ( x) = { − x − 4 − x 4 if x < − 4 x 4 − x 4 if − 4 ≤ x < 4 x 4 x − 4 if x ≥ 4 or simply, f ( x) = { − 2 x if x < − 4 8 if − 4 ≤ x < 4 2 x if x ≥ 4 Here is how it looks It could be f (x)=x^2, in which case y=x^24;




This Is The Graph Of Y F X For Each Of The Designated X Values In The Table Answer The Question Point X A X 1 X 2 X 3 X 4 X 5 X 6 F A Lim X Rightarrow A F X Lim X Rightarrow A



How Do You Graph F X 4 X 2 By Plotting Points Socratic



Trigonometry Graphs Graphing Functions Sparknotes



Quadratic Functions



Solved The Graph Of Y F X Is Given Graph The Indicated Function Graph Y F X 2 2 Select One Course Hero
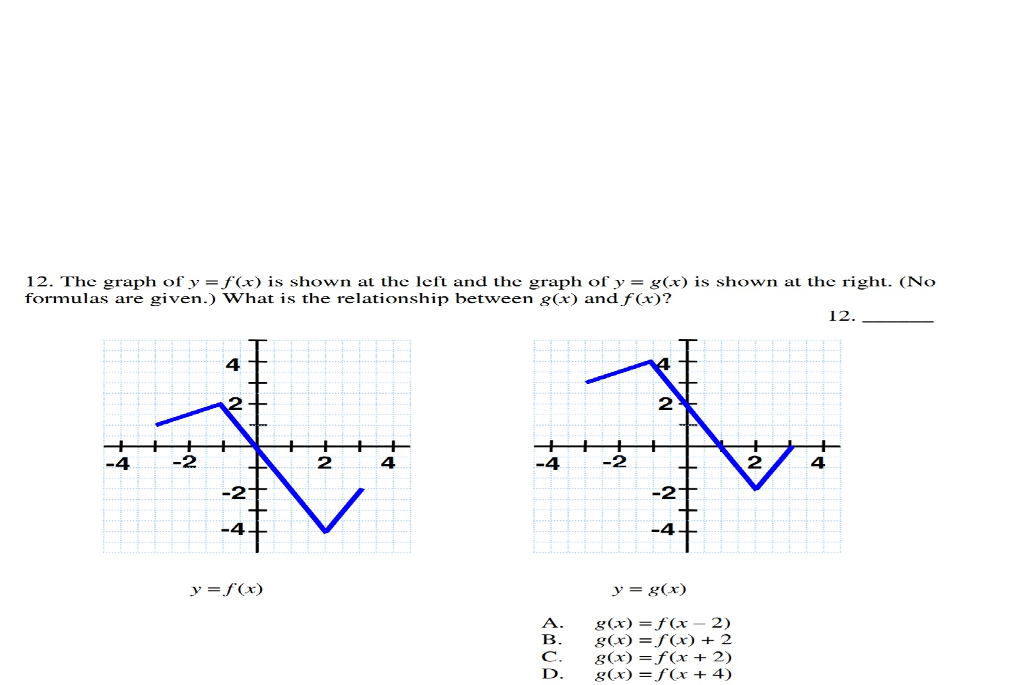



Solved 12 The Graph Of Y F X Is Shown At The Left And The Chegg Com



Answer In Algebra For Patrick J
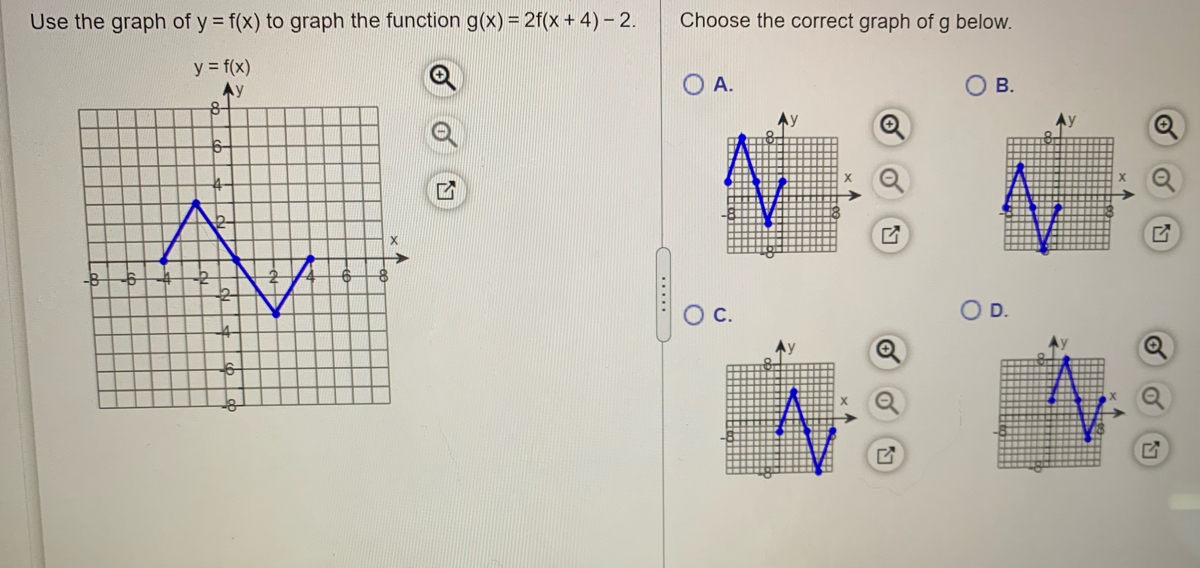



Answered Use The Graph Of Y F X To Graph The Bartleby



Solution Draw The Graph Of Y F X X 2 8x 7
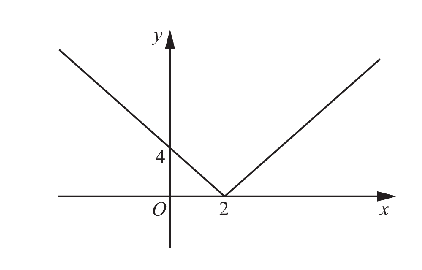



Cie Graph Additional Mathematics 18




Reflecting Functions Examples Video Khan Academy



How To Draw The Graph Of F X X 4 X 4 Quora




Explore Functions Cambridge Igcse Q3 Youtube
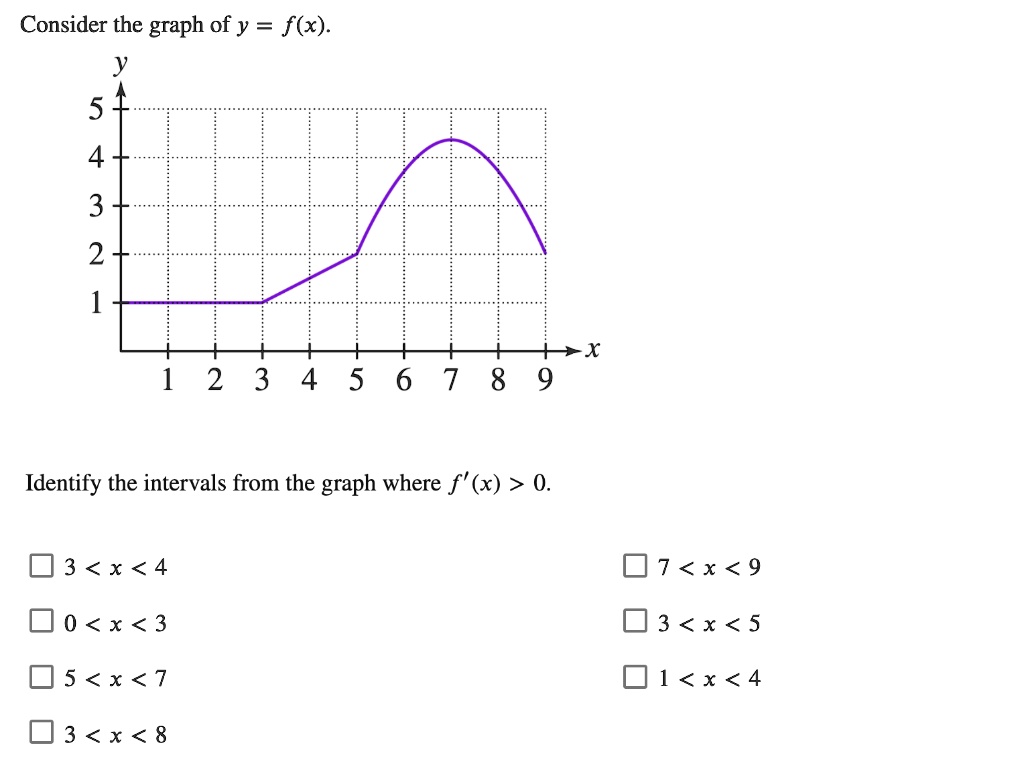



Solved Consider The Graph Of Y F X 5 4 3 2 X 2 3 4 5 6 7 8 9 Identify The Intervals From The Graph Where F X 0 3 X 4 07 X 9 D0 X 3 03 X 5 0s X 7 01 X 4 03 X 8
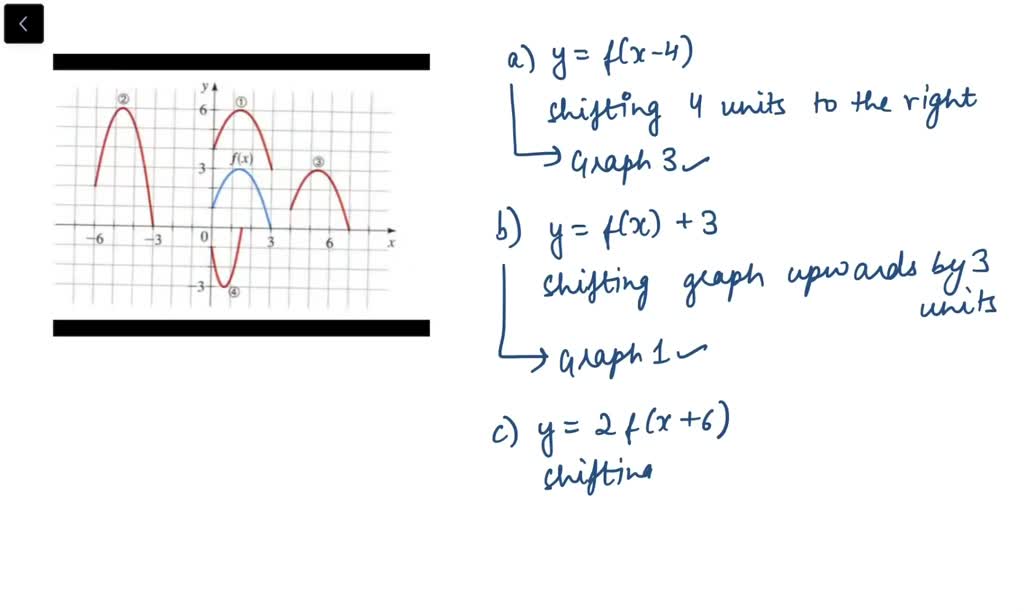



Solved The Graph Of Y F X Is Given Match Each Equation With Its Graph A Y F X 4 B Y F X 3 C Y 2 F X 6 D Y F 2 X



Y F X Graph




Best Answer The Graph Of Y F X Is Shown Below Find All The Values Of X Where F X 8 Brainly Com




The Diagram Shows The Graph Of The Derivative Of A Functin F X For 0 Le X Le 4 With F 0 0 Which Of The Following Could Be Correct Statements For Y



How Do You Graph Y 2 X 4 Socratic



Solved A Graph Of Y F X Follows No Formula For F Is Given Which Graph A B C Or D Represents The Graph Of Y F X 1 1 Course Hero




F X A X Y F X Graphs Of Related Functions 1 F X X 2 F X 2 X F X 5 X Vertical Translations Ppt Download
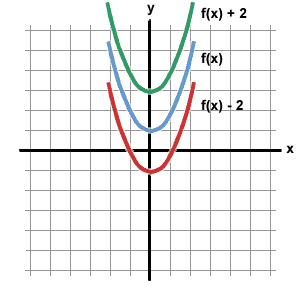



Honors Algebra 2 2nd Hour Fall 11 3 4 Functions Of Graphs




The Graph Of Y F X Is Shown Below Graph Y F 2x Wegglab



F X F X 2 F X 2



Fchsmrsneal Files Wordpress Com
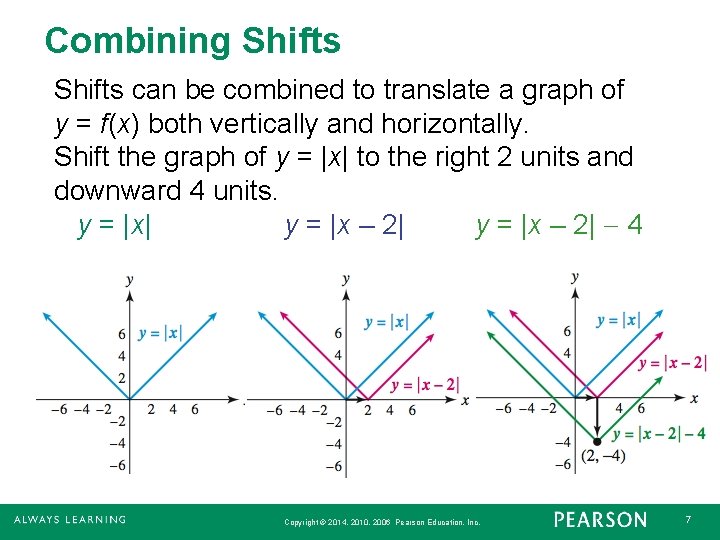



3 5 Transformations Of Graphs Graph Functions Using
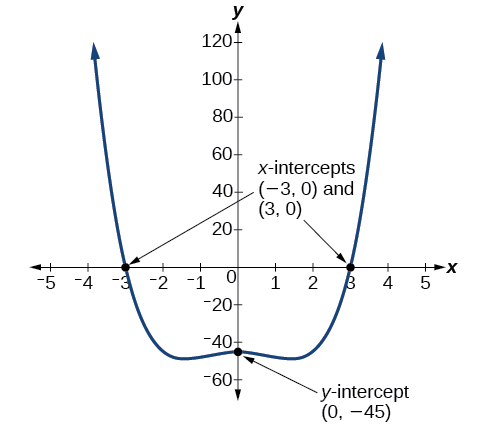



3 3 Power Functions And Polynomial Functions Mathematics Libretexts




Example 13 Define Function Y F X X 2 Complete The Table



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4




This Is The Graph Of F X 4 1 2 X What Is The Horizontal Asymptote Of F X Brainly Com
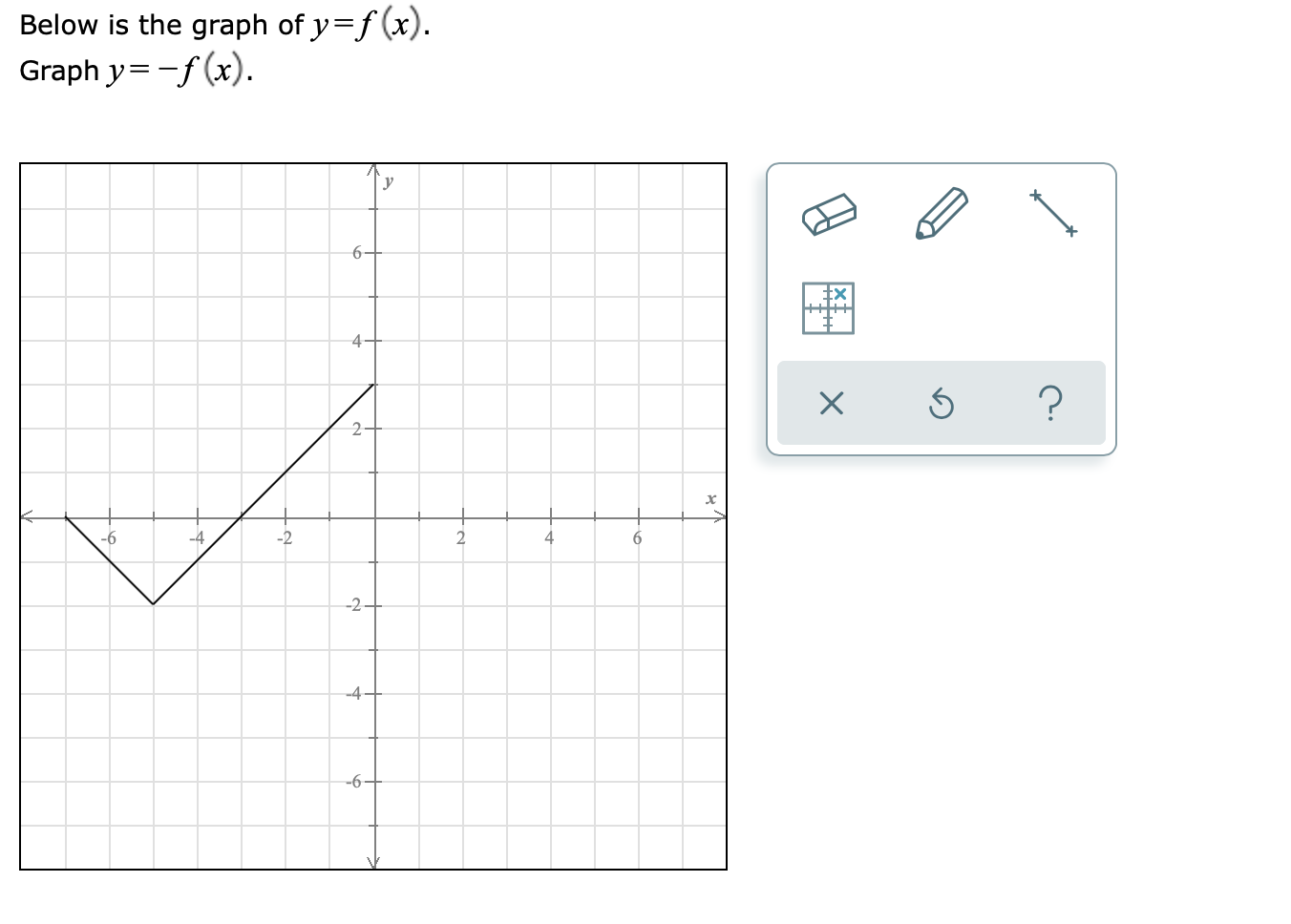



Solved Below Is The Graph Of Y F X Graph Y F X Y 6 X Chegg Com




Graph Quadratic Functions Using Properties Intermediate Algebra




An Explanation Of Graphical Modifications




Use The Graph Of Y F X To Find The Limits A Lim X To 4 F X B Lim X To 2 F X C Lim X To 1 F X D Lim X To 1 F X Study Com




Warm Up How Does The Graph Of Compare To Sketch Both To Confirm Ppt Download
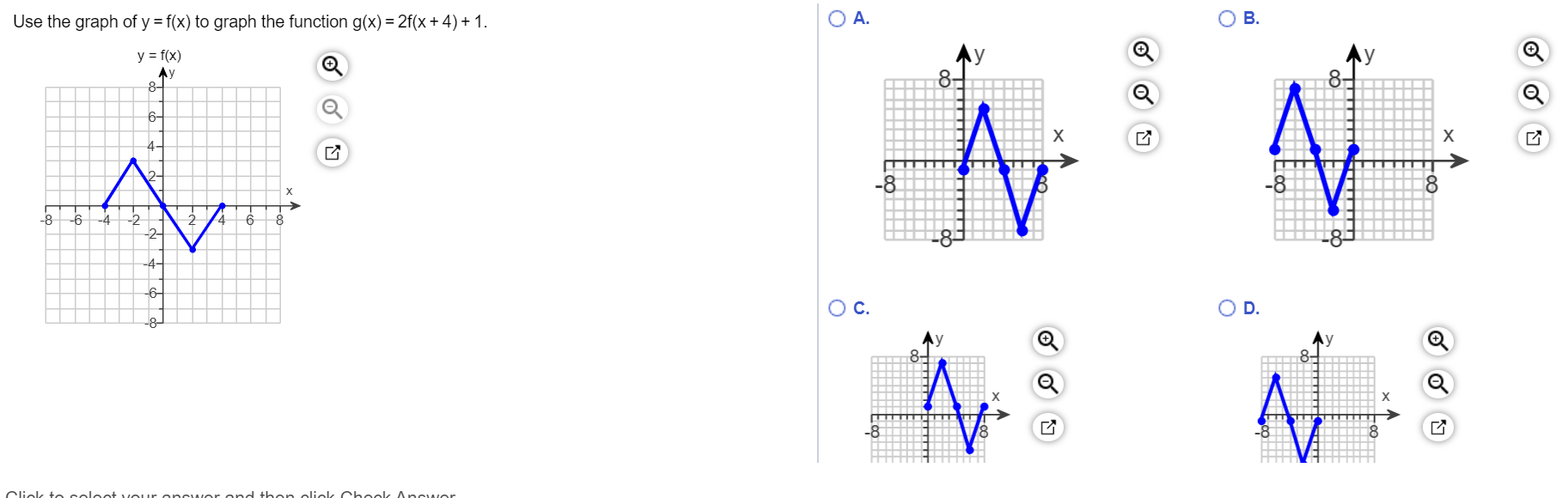



Solved Use The Graph Of Y F X To Graph The Function G X Chegg Com



Solution If I Was Given A Graph Of Y F X And The Graph Has Points 4 0 0 2 2 2 3 0 Connected In That Order How Would I Sketch The Graph Of Y F X 1




Graph Graph Inequalities With Step By Step Math Problem Solver



Graphing Quadratic Functions




Ppt F X A Powerpoint Presentation Free Download Id



26 The Graph Of The Function Y Fx Shown Here Is M Gauthmath



Practice Exam 1
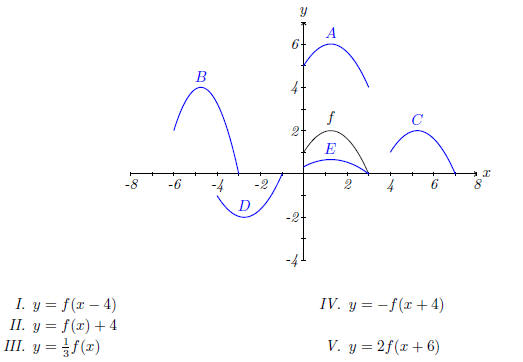



A Catalog Of Essential Functions



Secure Media Collegeboard Org



Graph Graph Inequalities With Step By Step Math Problem Solver




Sketch The Graph Of The Combined Function Of Y G F X For The Following Functions Of F X And G X Mathematics Stack Exchange
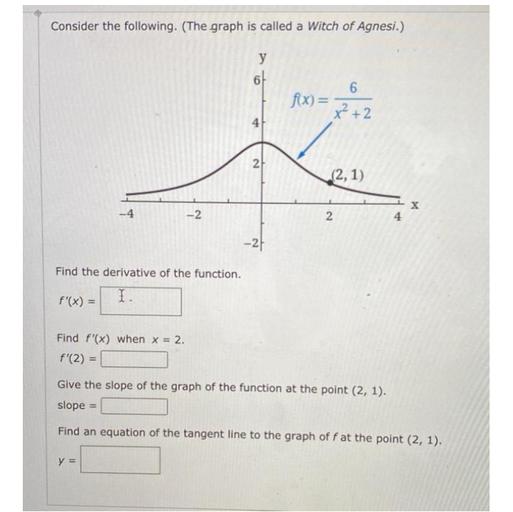



Consider The Following The Graph Is Called A Witch Of Math
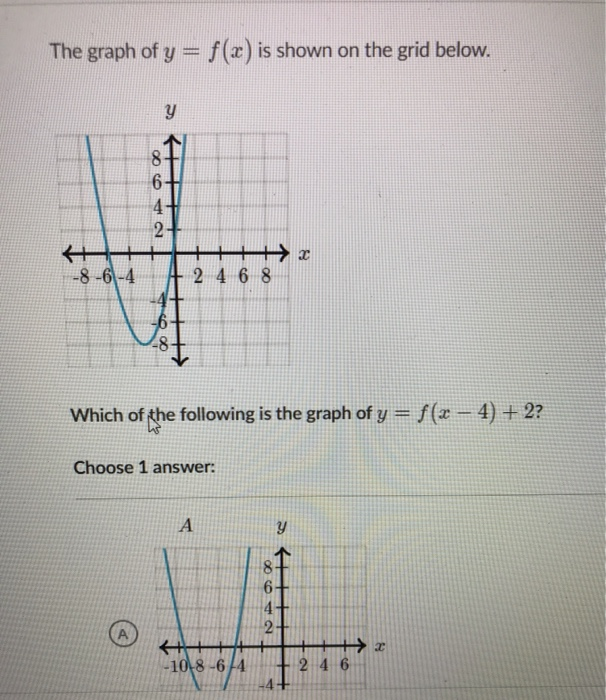



Solved The Graph Of Y F X Is Shown On The Grid Below Y 8 Chegg Com
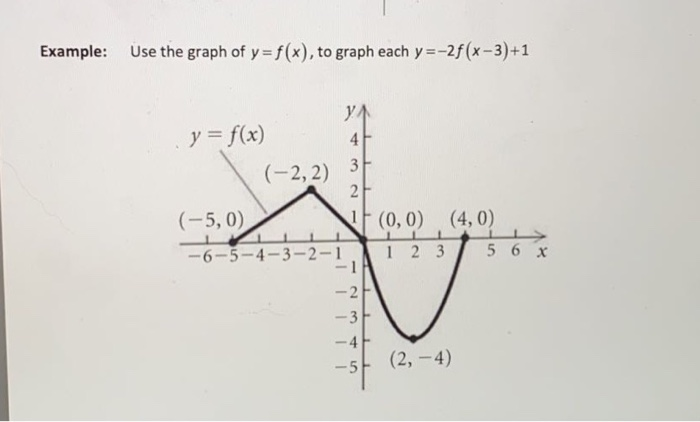



Solved Example Use The Graph Of Y F X To Graph Each Chegg Com



Graph Transformations
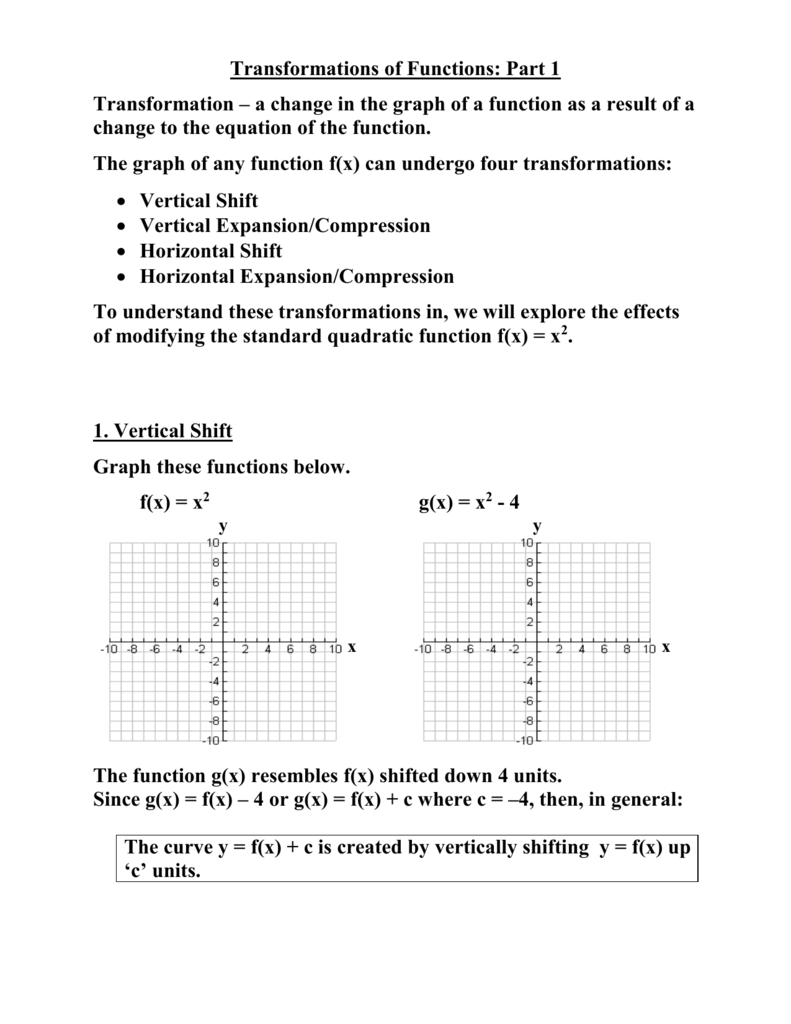



Transformations Of Functions Part 1
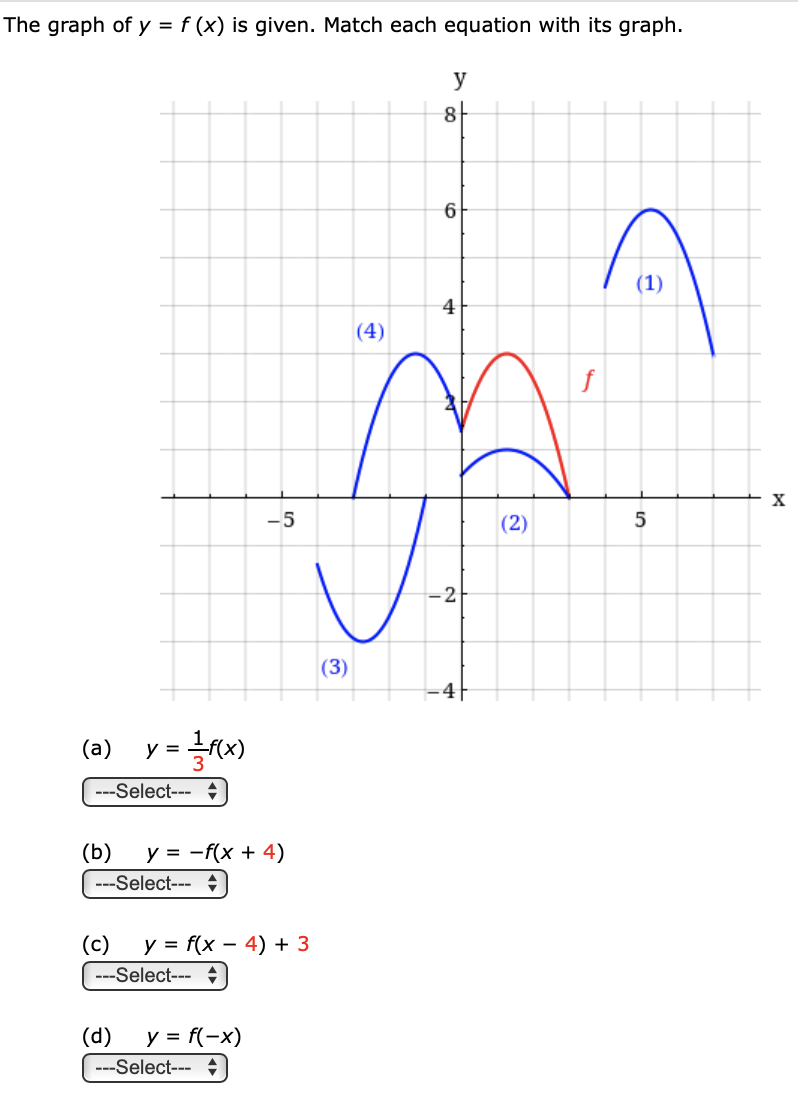



Answered The Graph Of Y F X Is Given Match Bartleby




Cc The Derivative Function



Daviddelgado Blogsek Es




The Graph Of Y F X The Derivative Of F X Is Shown Below Given F 4 2 Evaluate F 4 Brainly Com




Pc12 Sol C04 4 3



Quadratic Functions
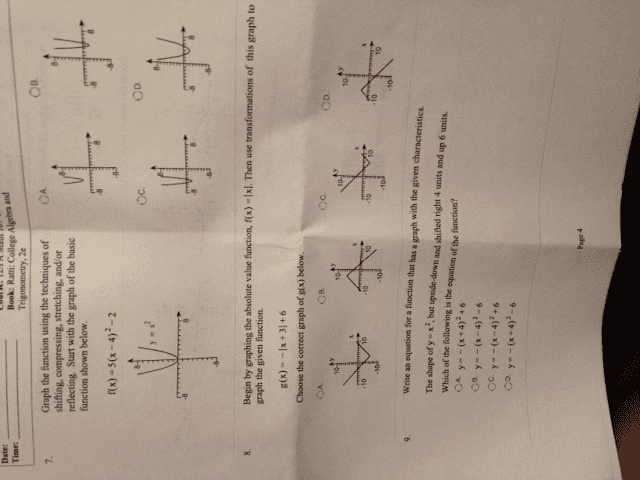



Oneclass Given The Graph Of The Line Represented By The Equation F X 2x B If B Is Increased By
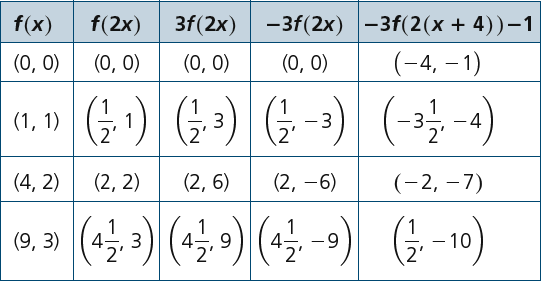



Using Transformations To Graph Functions Of The Form



Mrparrbccalculus Weebly Com
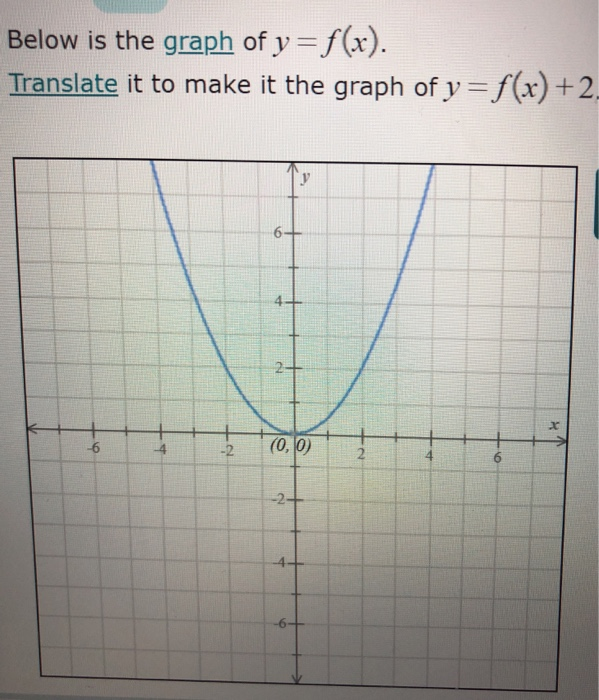



Solved Below Is The Graph Of Y F X Translate It To Make Chegg Com




Shifting Values On A Graph Mathematics Stack Exchange



Solved In 7 The Graph Of Y F X Is Given Graph The Indicated Function Course Hero



How Do You Find The Maximum And Minimum Of Y X 2 X 4 Socratic



Www2 Lawrence Edu
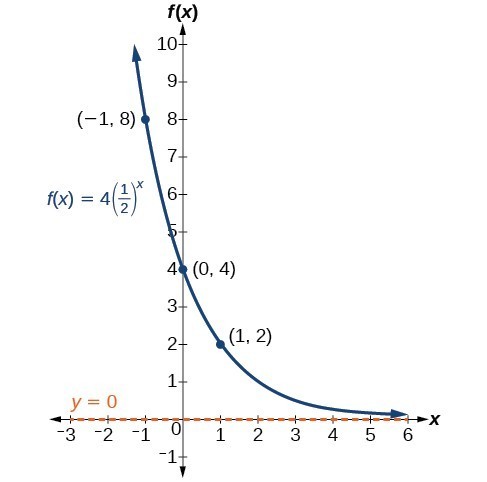



Graph Exponential Functions Using Transformations Math 1314 College Algebra



1
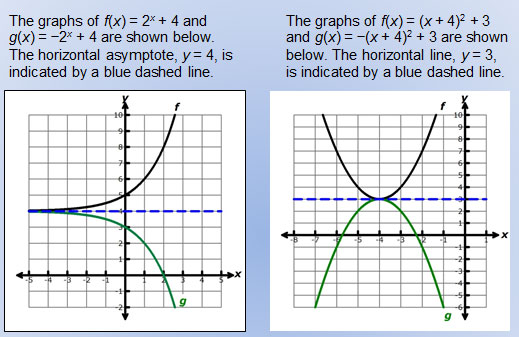



Untitled Document



Solution If P 4 5 Is A Point On The Graph Of The Function Y F X Find The Corresponding Point On The Graph Of Y 2f9x 6 Not Sure But I Think It Is 6 8 Thanks For




Sketch A Graph Of F X X 4 6x 2 Identify Local Extrema Inflection Points And X And Y Intercepts When They Exist Study Com
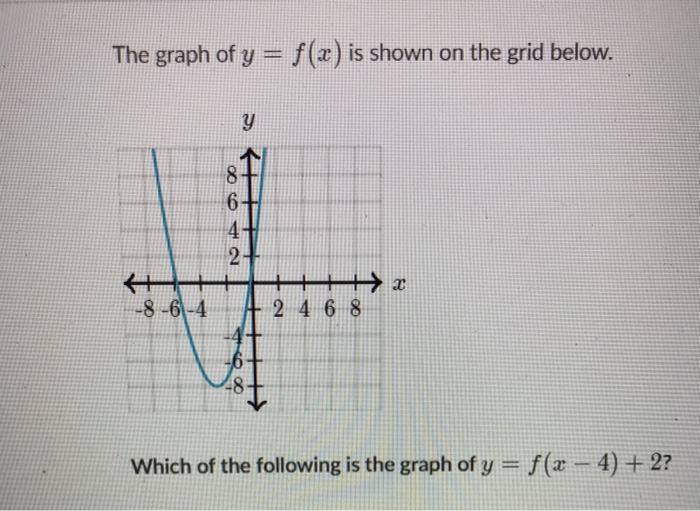



Solved The Graph Of Y F X Is Shown On The Grid Below Y 8 Chegg Com



How Is The Graph Of Y 1 3x 2 4 Related To The Graph Of F X X 2 Socratic



How To Draw The Graph Of F X X 4 X 4 Quora




Graphs Of Exponential Functions Lumen Learning College Algebra




Question Video Determining The Function Of A Translated Graph Nagwa



Translations Of A Graph Topics In Precalculus


