たとえば, 2 x 2 7 x 3, 6 x 2 7 x − 3 などは たすきがけ因数分解の公式を用いて因数分解することになります. その代わり,公式 x 2 ( a b) x a b = ( x a) ( x b) を用いるときには, 「かけて定数,和が1次」と標語的に考えることで因数分解できました 3乗が登場する因数分解を学ぶ前に、以下の3乗の計算を覚えてください。 これらの式は是非、覚えましょう。 右辺の値を見て、「これは を三乗したものだな」などとわかるようになることが大切です。 ちょっと多いなって人は くらいまでは頑張ってみ 因数分解の工夫(3)(難)(4乗と複二次式・たすき掛け) 解説 中3数学 因数分解 標準問題 発展問題 前回までの内容でも、難関レベルの問題に対応できると思うが、
たすきがけの因数分解 高校数学の無料オンライン学習サイトko Su
3次方程式 因数分解 たすきがけ
3次方程式 因数分解 たすきがけ-ステップ1 乗法公式を使おう(2分47秒) 4/6 ステップ2 x 2 の係数が1以外の場合(1分35秒) 5/6 ステップ3 「たすきがけ」を覚えよう(2分54秒) 6/6 ダンスでたすきがけを覚えよう! (32秒) x 2 の係数が1ではない2次方程式を因数分解するときに、とても 因数分解ができると、 二次以上の方程式を解く のに役立ちます。 因数分解の公式 ここでは、因数分解の \(2\) 乗の公式および \(3\) 乗の公式を確認していきます。 2 乗の公式 二次式を因数分解する公式は以下の通りです。




因数分解 たすきがけ 難問 の思考手順 怜悧玲瓏 高校数学を天空から俯瞰する
因数分解の電卓 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。 連立方程式の電卓 2つの方程式を入力することで連立方程式として解くことができる電卓です。 たすき掛けで因数分解したくても、適した数が見つからない! 2次の因数分解の話ですが、「たすき掛けで因数分解できない!」こんなことありませんか? たすき掛けのやり方は習って知っている、でも、答えが見つからない! 例えば、\ 二次方程式の因数分解で、暗算が得意な人は、たすき掛けを使いません。 たすきがけを使わないで暗算でする方法の概要 (二乗の係数が2の場合)因数分解後の(2Xa)(Xb)の候補a,bについて、次の3つの場合に分けて解説します。 候補が1種類の場合ただし、(2Xa)(Xb)と、逆の(2Xb)(Xa)の2通りを考える。
たすきがけの因数分解について解説してきました。 たすきがけは優秀な因数分解の方法だが、 当たりを探す必要 がある 数字が大きくなると たすきがけでは 当たりを引けない可能性 が出 たすきがけによる因数分解 たすきがけとは,二次式を因数分解するための方法です。たすきがけを使って 3 x 2 − 10 x 8 3x^210x8 3 x 2 − 10 x 8 を因数分解してみましょう。 手順1 かけて 3 3 3 (二次の係数)になる2つの整数を適当に決めて左に縦に並べる 手順2 今回は2次方程式の解き方の発展問題を扱う。 前回 ←2次方程式の解き方と練習問題(2)(標) 次回 →2次方程式の解き方(補足)(二元二次連立方程式)(難) 解き方の前回 ← 31 2次方程式の解き方 311 基本的な2次方程式の解き方(1)(基) 312 2次方程式のの解き方(2)(展開・置き換え・二乗利
(ii)ax 2 bxcの因数分解はたすきがけで行う。つまり つまり ア×ウ=a , イ×エ=c , ア×エ+イ×ウ=bとなる数を見つければ(アxイ)(ウxエ)と因数分解できる。 たすき掛けの因数分解になるまでねばってみよう笑 Step5 因数分解っぽくする たすき掛けもいよいよ終盤。 たすきがけの組み合わせがわかったら、 因数分解っぽい形にしてみよう笑 たすき掛けで書き出した数字のうち、 いちばん左のやつが xの係数 、 中3数学の二次方程式の問題で ①x22x+1=0 ② (x1)2=0 (2は二乗です) ③ x1=0 ④ x=1 と、なるそうなのですが なぜ②から③に行く間に二乗が取れて「x1=0」になるのですか? 教えて




たすきがけの因数分解のやり方 問題付き 理系ラボ




2次方程式の 解の公式 の導出と 公式の使い方を具体例
大きな因数分解の準備として,定数項だけの小さな因数分解をする. 2 x 2 (7y−1) x (3y−1)(y1) ここからが全体の大きなたすき掛けとなる. 多項式の基本6|3次以上の展開と因数分解の公式の総まとめ 前々回の記事で説明したように,たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は,いったん解を求めることによって因数分解できるのでした. では,3次式では因数分解 複数の文字を含む因数分解は最も次数が低い文字で整理せよ 次の式を因数分解せよ 複数の文字を含む因数分解 以下の3つの条件を満たす問題は,\ 闇雲に考えているだけでは手も足も出ない 複数の文字が含まれている 一見して公式の形ではない



たすきがけのやり方について 数学 苦手解決q A 進研ゼミ高校講座




たすきがけの因数分解のやり方 問題付き 理系ラボ
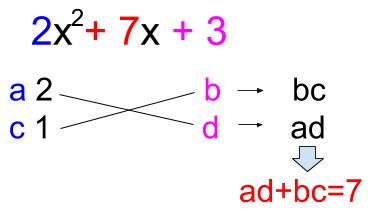
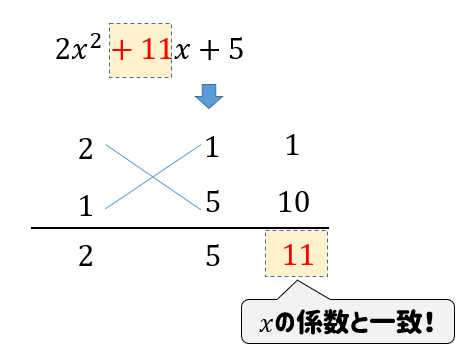
の問題の因数分解(たすきがけ)についてですね。 解説 5 x 2 11 x 2☆は、 acx 2 ( ad bc ) x bd =( ax b )( cx d )を使って因数分解しますが、『たすきがけ』を使うとうまく a 、 b 、 c 、 d が見つかります。 2次3項式ax²bxcの因数分解(たすき掛け) 因数分解公式と3次式の因数分解① 因数分解公式と3次式の因数分解② a³b³c³3abc たすき掛け(たすきがけ)とは、 二次式を因数分解するためのテクニック の \(1\) つです。 たすき掛け \(Ax^2 Bx C = (ax b)(cx d)\) と因数分解できるとき、\(a\), \(b\), \(c\), \(d\) を以下のように求める方法を「たすき掛け」という。



たすき掛け因数分解



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス
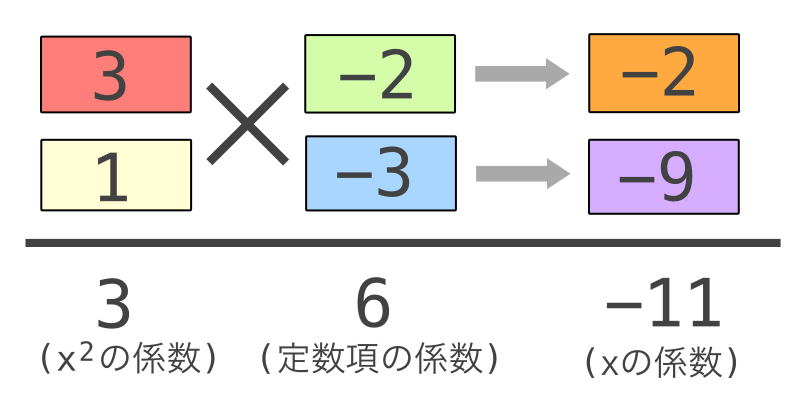
掛けると 3y 2 2y−1 となる式を考えるとは, 3y 2 2y−1 を因数分解しておくということ: (3y−1) (y1) このように準備しておいて、前2つ、後ろ2つの係数の組合せのうちで、1次の係数が 7y−1 に一致するものを探す。 たすき掛けの計算は、次の計算を省略したたすき掛けに代わる新しい因数分解の方法として、「取って掛け」という方法が知られてい る。 (例) 6x 2 -7x-3 を因数分解する場合、x 2 の係数6を取って、定数校-3に掛けた2次 式 x 2 -7x-18中3数学をバッチリ攻略!因数分解・平方根・二次方程式 たすきがけによる因数分解は覚えなくてもいい 高校数学の 因数定理を用いた因数分解のコツとは?因数の見つけ方(候補)も 因数分解のやり方・公式と解き方のコツ教えます!高校レベル



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス



たすきがけのやり方について 数学 苦手解決q A 進研ゼミ高校講座
ベーシック数学 eテレ 毎週 月曜日 午後2:00〜2:10 ※この番組は、前年度の再放送です。 出演者紹介;どちらの文字で整理してもたすきがけ因数分解から逃れられません。 どのタイミングでたすきがけになるかが異なります。 自分が解きやすいほうでどうぞ。 どちらで解いても楽勝!というのがベストです。 例題4 次の式を因数分解しなさい。 \(2x^27xy3y^2 ゆうき先生 たすきがけ因数分解で二次方程式を解く5つのステップ たすきがけ因数分解で二次方程式は解ける?? ある日、数学が苦手なかなちゃんは、つぎの二次方程式に出会いました。




因数分解難問と意外な別解 怜悧玲瓏 高校数学を天空から俯瞰する
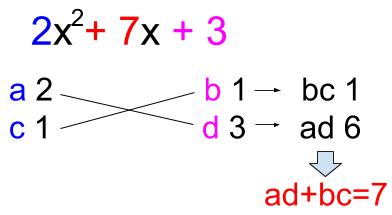



たすきがけの因数分解 高校数学の無料オンライン学習サイトko Su
因数分解をするときに使う上の左図のような図のことを「たすきがけ」といいます。 これでx 2 に係数がある場合も、パパっと因数分解できますね☆問題2 3次方程式 $x^{3}4x3=0$ を解け。(1) 左上のカギ括弧に、定数項=$3$の約数の中から$x=1$を書く。 (2) 組立除法を実行すると、商は$x^{2}x3$で余りは$0$と分かる。 (3) この商はたすき掛けができなさそうなので、本当に因数分解できないかを確認するために判別式例5 2次方程式 02 x 2 -07 x+06=0を解け。 両辺に10をかけて,2 x 2 -7x+6=0 (x-2)(2 x-3)=0 よって,x=2, 例3,例4,例5では,各係数をすべて整数で,x 2 の係数を正にするように,方程式の両辺に定数をかけている。 そうすることによって,整数を係数とする1次式の積に因数分解
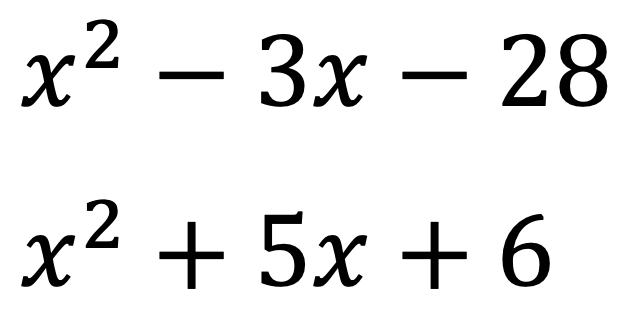



中学高校数学 たすきがけ 因数分解 の裏ワザ 東大 桐生雄大 Note




因数分解 たすきがけ 難問 の思考手順 怜悧玲瓏 高校数学を天空から俯瞰する
応用分野: 2次方程式の解き方, 因数分解 たすきがけ手法による因数分解の手順 2次関数 a x 2 b x c ホーム>>カテゴリー別分類>>数と式>>整式:たすきがけ手法による因数分解 x³6x²11x6 = (x2)(x²4x3) とわかりました。 2次方程式まで次数を下げていこう ここまで来れば、x²4x3を因数分解すればいいだけなので簡単です。 たすきがけなり、解の公式を使うなりして求めましょう。 x²4x3 = (x1)(x3) 以上より、 f(x) =x³6x²11x6 =(x2)(x²4x3)たすきがけによる因数分解の手順と方法 最初にまず、 たすきがけの方法がどうやってつくられているのか のお話もしようと思います。 「展開せよ」という指示がありますが、いまご覧いただいている式のかたちはもう、因数分解された形になっています。



三次式をたすきがけを用いて因数分解をする方法がわかりません Yahoo 知恵袋



因数分解 簡単に計算できる電卓サイト
3/6 ステップ1 乗法公式を使おう(2分47秒) 4/6 ステップ2 x 2 の係数が1以外の場合(1分35秒) 5/6 ステップ3 「たすきがけ」を覚えよう(2分54秒) たすきがけを使って因数分解してみよう! では実際にたすき掛けを使って因数分解してみましょう。 (1)x²4x3 =(x1)(x3) (2)2x²11x5 =(x5)(2x+1) (3)4x²5x21 =(4x7)(x3) 最後に、因数分解の手順をおさらい例 6 ⅹ 2 + 7 ⅹ- 3 を 2 次方程式の解を用いて因数分解する。 これは、たすきがけでも簡単に因数分解できるが、 6 ⅹ 2 + 7 ⅹ- 3 = 0 とおいた方程式の解を解の公式でもとめ、上の因数分解の式を利用するという方法を理解するための例。




数学 因数分解 たすき掛け 問題




例題で学ぶ高校数学 未分類
となり、xを含まない部分を因数分解することを考えます。2y 2 y 3 = (2y 2 y 3) と変形すると、カッコの中は、 y 2 y の形をしているので、たすきがけをして因数分解をします。 すると、2y 2 y 3 = (2y 3)(y 1) と変形できますね。分解とは、1つにまとまっているものをいくつかのものに分けることです。 ですので、この、因数分解という言葉は簡単にまとめてしまえば、 式を展開 することの逆バージョンであるといえます。 例えば、15という数は、 3×5 で表されます。 この3や5の>> 第13回 2次方程式 たすきがけによる因数分解;




最新因数 分解 たすき がけ 練習 問題 最高のカラーリングのアイデア



因数分解の方法 公式と問題のまとめ たすき掛けや応用的なコツも解説
今回の学習 第13回 2次方程式 たすきがけによる因数分解Title 2次方程式の徹底100問 Author 4278 Last modified by 奥 淳 Created Date AM Other titles 2次方程式の徹底100問 この多項式は次のように因数分解できますね。 よって、f (x)は因数として(x1)と (x3)をもつわけです。 ここで因数定理における (xa)の「a」として、「3」を使ってみることにします。 f (x)にx=3を代入すると、 見事にf (3)=0となりました! このように、f (x)の因数がわかっているときに、f (x)=0の解がわかるというのが因数定理の「f (x)が因数として (xa)をもつ




因数分解 たすきがけ や3乗の因数分解のやり方を解説 ますますmathが好きになる 魔法の数学ノート




たすきがけを使った因数分解 Youtube



因数定理をパパッと理解 因数の見つけ方と問題の解き方も紹介 Studyplus スタディプラス




数と方程式 3 難しい因数分解 交代式 数i A 東大数学9割のkatsuyaが販売する高校数学の問題集




3次式の因数分解 公式とやり方について問題を使って解説 数スタ



1




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す



たすき掛けの因数分解 コツを学んでやり方をマスターしよう 数スタ




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す




たすきがけの仕方とは 因数分解を早くするコツを問題6選で解説します 遊ぶ数学



因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト



たすき掛けのやり方を徹底解説 因数分解の計算問題 受験辞典




X 2xy Y 2x 2y 8 答えは X y 2 X y 4 Clear
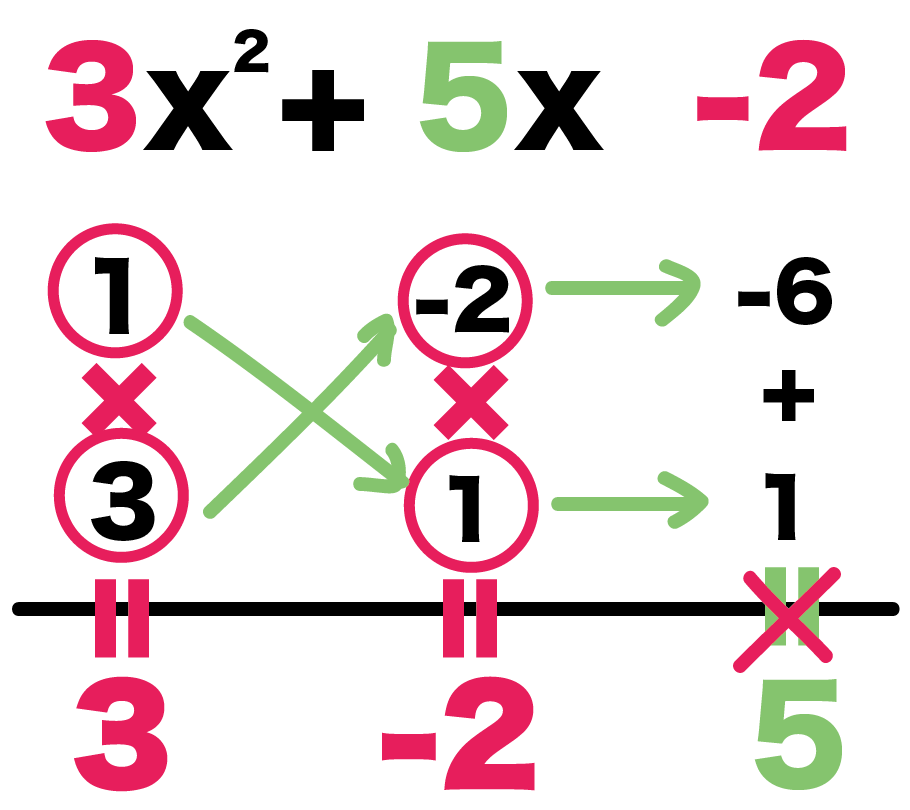



中学数学 たすき掛け因数分解のやり方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




高校数学 たすきがけを使う因数分解 映像授業のtry It トライイット



因数分解とは 公式と計算のやり方を覚えて問題を解いてみよう 中学 高校数学 テラコヤプラス By Ameba




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す




たすきがけ因数分解で二次方程式を解く5つのステップ Qikeru 学びを楽しくわかりやすく




3次以上の展開と因数分解はどうなる 公式の総まとめ




因数分解の方法 公式と問題のまとめ たすき掛けや応用的なコツも解説




高校数学 2次3項式ax Bx Cの因数分解 たすき掛け 受験の月




小技 2次式の因数分解 たすきがけ Youtube




たすきがけの因数分解 高校数学の無料オンライン学習サイトko Su



3



2文字のたすき掛け




たすきがけによる因数分解は覚えなくてもいい 高校数学の美しい物語



たすきがけできない二次方程式を どうやって因数分解しろっていうんですか Yahoo 知恵袋




3乗の因数分解 展開 公式 理系ラボ




因数分解 たすきがけ や3乗の因数分解のやり方を解説 ますますmathが好きになる 魔法の数学ノート



因数分解による方法 中学から数学だいすき




因数分解 たすきがけ や3乗の因数分解のやり方を解説 ますますmathが好きになる 魔法の数学ノート
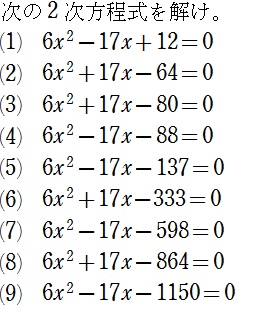



因数分解 たすきがけ 難問 の思考手順 怜悧玲瓏 高校数学を天空から俯瞰する




3次式の因数分解 公式とやり方について問題を使って解説 Youtube




たすきがけの因数分解のやり方 問題付き 理系ラボ




高校数学 数 9 因数分解 たすき掛け編 Youtube



因数分解とは 公式や計算のやり方 問題の解き方 受験辞典




数と方程式 2 複雑な因数分解 数i A 東大数学9割のkatsuyaが販売する高校数学の問題集



たすき掛け因数分解




たすきがけの因数分解のやり方 問題付き 理系ラボ



たすき掛けのやり方を徹底解説 因数分解の計算問題 受験辞典
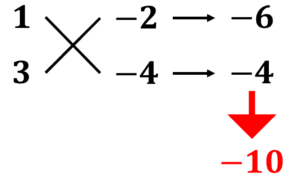



たすきがけによる因数分解は覚えなくてもいい 高校数学の美しい物語



たすきがけ 数学 の因数分解で二次方程式を解く手順と方法 簡単な練習問題 猫に数学




たすきがけの因数分解のやり方 問題付き 理系ラボ
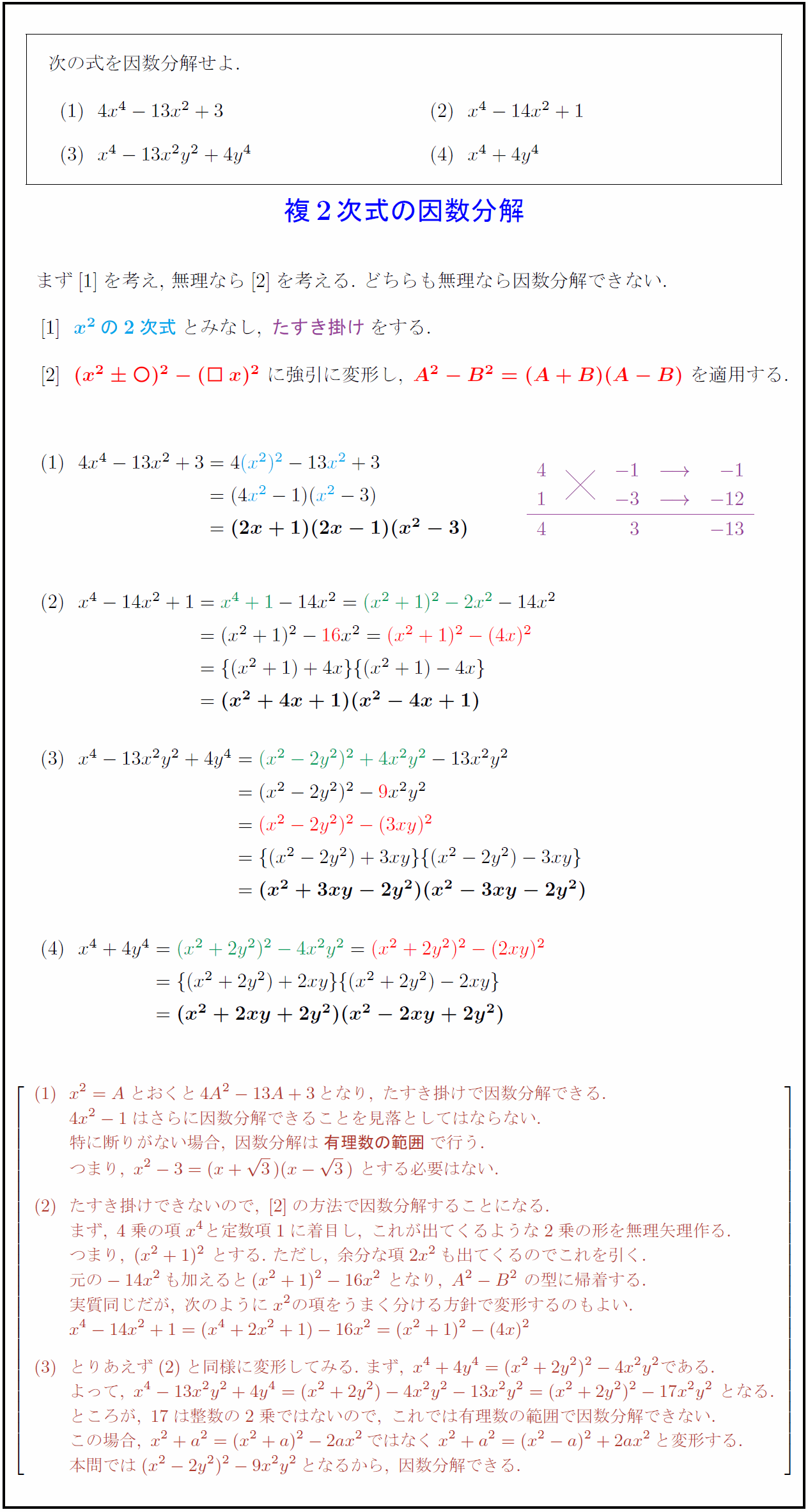



高校数学 複2次式 2乗の2次式ax Bx C の因数分解 受験の月



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス



3
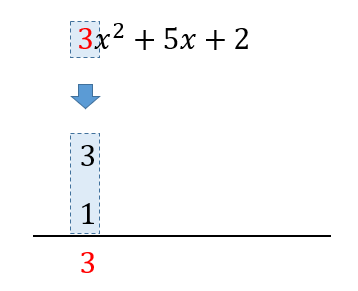



たすき掛けの因数分解 コツを学んでやり方をマスターしよう 数スタ




最新因数 分解 たすき がけ 練習 問題 最高のカラーリングのアイデア




たすき掛けのやり方 因数分解がスラスラ解けるようになる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学 複数の文字を含む因数分解は最も次数が低い文字で整理せよ 受験の月




因数分解 3 たすきがけ は不要か 怜悧玲瓏 高校数学を天空から俯瞰する




たすきがけ因数分解 はどう便利 コツを具体例で解説




たすきがけの因数分解のやり方 問題付き 理系ラボ




高校数学 A 因数分解のたすき掛けを一発で求めるコツ やはり俺の考察ブログはまちがっている アニメ 数学




高校数学 因数分解のたすきがけ問題を早く解くコツは どんなたすきがけもラクラク




たすき掛けによる因数分解のコツとは 大学入試数学の考え方と解法




Juken Mikata Sakura Ne Jp Wp Content Uploads




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト




因数分解 2 たすき掛け 数 宇宙を歩く高校数学 基礎




高校数学 高次方程式の解法 1 練習編 映像授業のtry It トライイット




高校数学 数 11 因数分解 3次式の公式編 Youtube




高校数学 因数分解公式と3次式の因数分解 受験の月
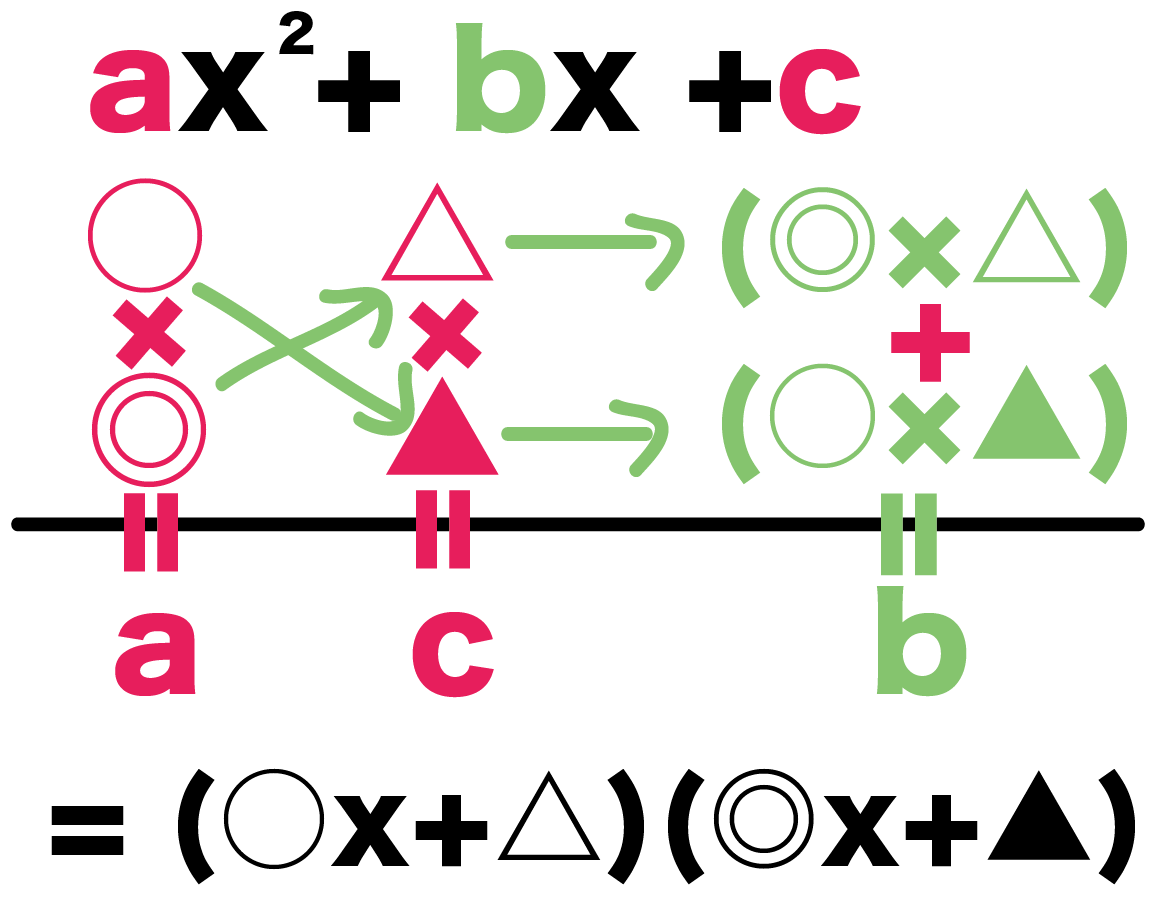



中学数学 たすき掛け因数分解のやり方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




因数分解のやり方がわからない人必見 公式や解き方のコツをわかりやすく紹介 高校生向け受験応援メディア 受験のミカタ



1
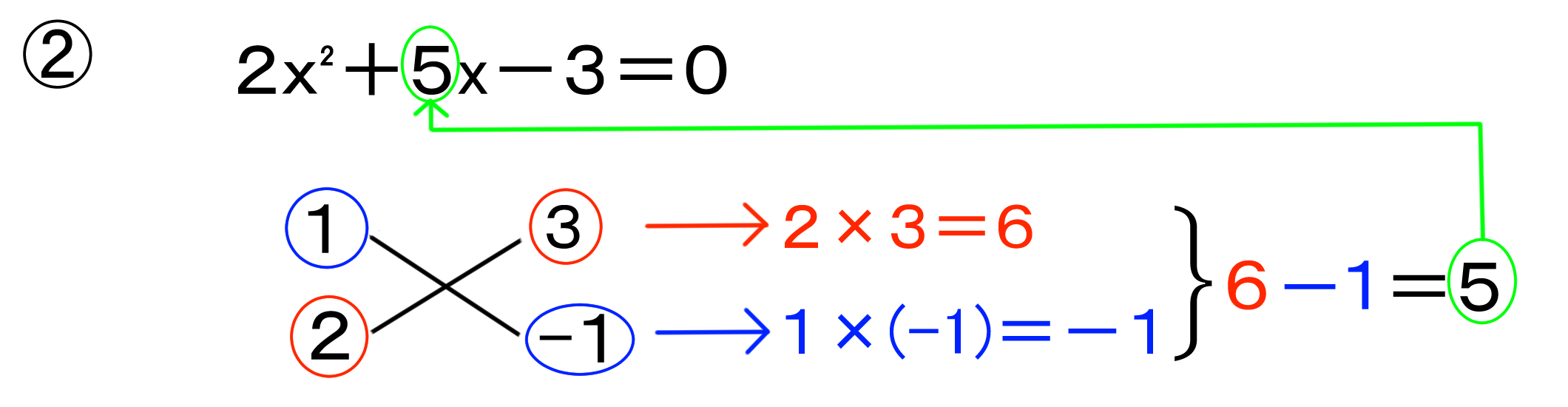



難しい因数分解も たすきがけ で簡単に この裏技で2次方程式も楽に解ける バカでもわかる 中学数学




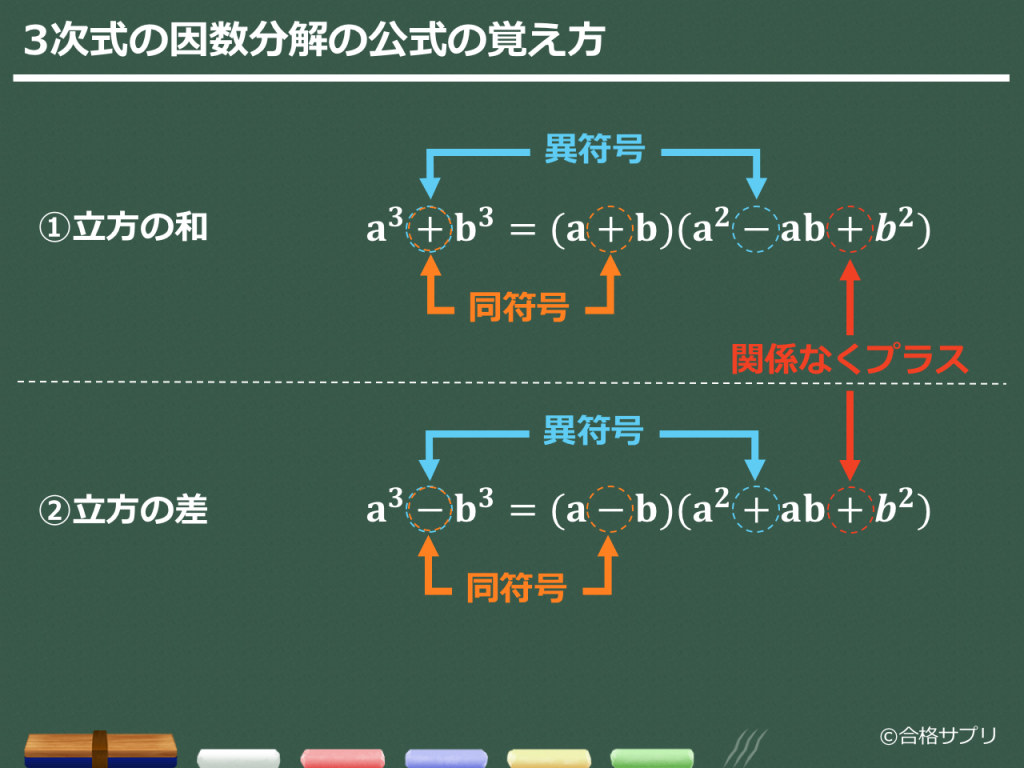
3分で分かる 因数分解の公式と解き方のコツ 練習問題と解説をわかりやすく 合格サプリ




新高1生へ 失敗しないたすきがけ因数分解 Youtube




たすき掛けの因数分解 コツを学んでやり方をマスターしよう 数スタ




たすきがけの因数分解のやり方 問題付き 理系ラボ



4次方程式の具体的解き方




3分で分かる 因数分解の公式と解き方のコツ 練習問題と解説をわかりやすく 合格サプリ



たすきがけ 数学 の因数分解で二次方程式を解く手順と方法 簡単な練習問題 猫に数学




因数分解 発展 三次式の因数分解 On Vimeo
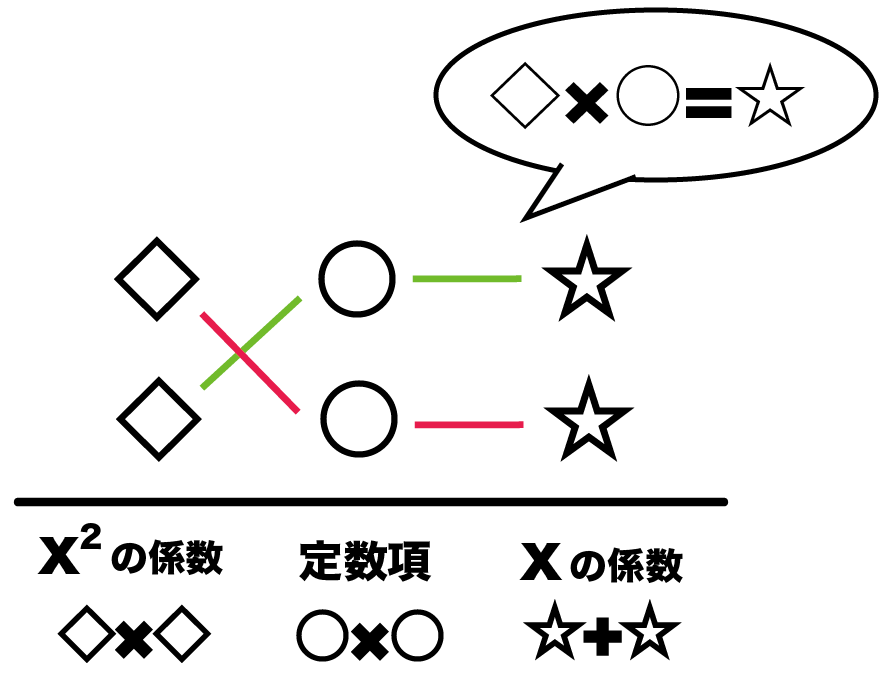



たすきがけ因数分解で二次方程式を解く5つのステップ Qikeru 学びを楽しくわかりやすく




数学も英語も強くなる 意外な数学英語 Unexpected Math English Crisscross Method



3分で分かる 因数分解の公式と解き方のコツ 練習問題と解説をわかりやすく 合格サプリ




たすきがけ というものを使うみたいですが やり方が分かりません Clear




たすきがけ因数分解で二次方程式を解く5つのステップ Qikeru 学びを楽しくわかりやすく
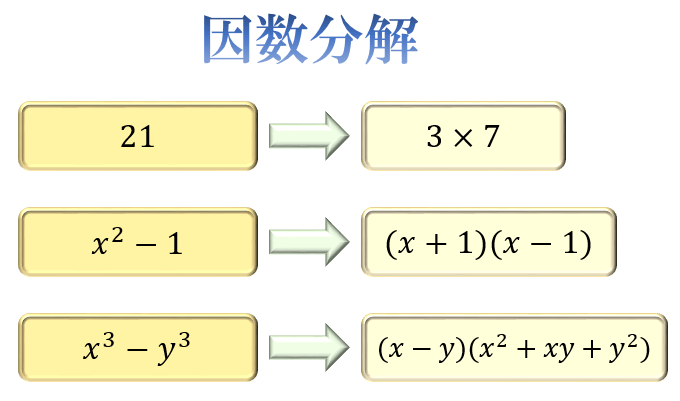



因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ



因数分解 たすきがけ 難問 の思考手順 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 たすき掛けの因数分解 数樂管理人のブログ




因数分解 4 スーパーたすきがけ 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月




数学 質問解答 高校生の因数分解 複雑な式のたすきがけ 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生


