Integration by using substitution methods👍 Correct answer to the question 5/x3/y=1 and 3/2x2/2y=5 by substitution method eanswersin Substitution Method in Formulas You will also see problems on your algebra exam that ask you to use the substitution method in a formula In addition, you will need to use the substitution method in this way on the geometry part of the exam Example The area of a triangle is A = (base × height) ÷ 2
Using Matrices Solve The Following System Of Equations 2x 3y 5z 11 3x 2y 4z 5 X Y 2z 3 Quora
5/x-3/y=1 3/2x 2/3y=5 by substitution method
5/x-3/y=1 3/2x 2/3y=5 by substitution method-2 algebraic methods (elimination and substitution) and graphical method Elimination 2x 3y = 5 So 6x 9y = 15 (equation 1) 3x y = 4 6x 2y = 8 (equation 2) (6x 9y) (6x 2y) = 15 8 7y = 7 y = 1 (equation 3) Substitute y = 1 into equati X y=5 2x3y=5Question 1 Solve the following pair of linear equations by the elimination method and the substitution method (i) xy=5 and 2x 3y = 4 (i) 3x 4y = 10 and 2x 2y = 2 (iii) 3x 5y 4 0 and 9x = 2y 7Begin with 2x 3y = 5 Subtract 2x from each side3y = 5 2x Divide both sides by 3 y = 5/3 2x/3 Usually, you want to avoid leading your solution with a negative, so it



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora
5/x3/y=1, 3/2x2/3y=5 Find the value of x,y by substitution method 1 See answer anjanigmailcom is waiting for your help Add your answer and earn points 1 See answer vaibhav is waiting for your help Add your answer and earn points Brainly UserBrainly User Answer ️3/2x2/3y=5(1) ️ 5/x3/y =1(2) ️Multiplying by 3 in equation (1) and by 2/3 in equation (2) we get,Miranda05masso miranda05masso Mathematics Middle School answered 2x8y=4 x=−3y5 substitution method 2
The given equations are `(3)/(2x) (2)/(3y) = 5` and `(5)/x (3)/y` = 1 Let `(1)/x = "a" and (1)/y = "b"` Then, we have `(3)/(2)"a" (2)/(3)"b"` = 5Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history2x=23y by substitution method About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features ©
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 5x2y=3;y=2x Tiger Algebra SolverSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Ex 36, 1 Solve the following pairs of equations by reducing them to a pair of linear equations(i) 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6Let 1/𝑥 = u 1/𝑦 = v So, our equations become1/2 u 1/3 v = 2 (3𝑢 2𝑣)/(2 × 3) = 2




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Frank Solutions For Class 9 Maths Chapter 8 Simultaneous Linear Equations Free Pdf
How do you solve #12y3x=1# and #x4y=1# using the substitution method?3x2y=12,xy=5 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 3x2y=12 Choose one of the equations and solve it for x by isolating x graph the points using these two linear equations 3xy=10 and 2xy=5 asked in ALGEBRA 2 by skylar Apprentice graphinglinearequations;




3 2x 2 3y 5 1 5 X 3 Y 1 2 Question On Simultaneous Linear Equation Solve This By Reducible To Pair Of Equation Method And Cross Maths Simultaneous Linear Equations Meritnation Com



Solve The Following Systems Of Equations 1 7x 1 6y 3 1 2x 1 3y 5 Sarthaks Econnect Largest Online Education Community
Solve this system of linear equaiton by an algebraic method So If I had to solve this the elimination method way, how would I do it? Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 − 6)/5 x = (25 − 6)/5 x = 𝟏𝟗/𝟓 Hence, x = 19/5,𝑦=6/5 Ex 34, 1 (SubstitutionAnswer to Solve each system by multiplying 1 2x3y=5 x2y=1 2 3xy=2 8x2y=4 3 2x5y=22 10x3y=22 4 4x2y=14 7x3y=8 By signing up,



Simultaneous Equations Gmat Math Study Guide




Ch 3 5 Elimination Multiplication Ppt Download
5 X 3 Y 1 3 2x 2 3y 5 Find The Value Of X Y By Substitution Method To Be A Brainliest Brainly In 3 2x 2 3y 5 1 5 X 3 Y 1 2 Question On Simultaneous Linear Equation Solve This By Reducible To Pair Of Equation Method And Cross Math Simultaneous LinearX=−3y5 substitution method Get the answers you need, now!Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




5 X 3 Y 1 3 2x 2 3y 5




Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy
Xy=3 3yx=5 Substitution Solve for x and y, using substitution method 2x y = 7, 4x 3y 1 =0 Find each of the following products (i) (x 4)(x 4) (ii Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers bySolve by using substitution method 3/2x5/3y=7 9x10y=14




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
Solve the system of equations by using the method of cross multiplication 2x 5y – 1 = 0, 2x 3y – 3 = 0The following steps will be useful to solve system of linear equations using method of substitution Step 1 In the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3SOLUTION Solve using the substitution method x32x=6 3x=6 x=36 x=3 #5 st=5 s=133t sol let, st=5 eq(i) s=133t eq(ii) substitute the value of s from eq(ii) in eq(i) (133t)t=5 132t=5 135=2t 8=2t t=4 #6 xy=4 y=2x sol let,
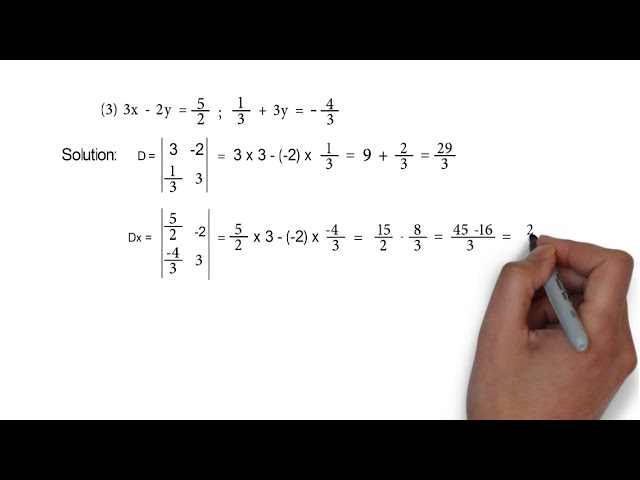



3x 2y 5 2 And 1 3 3y 4 3 Problem Set 1 Q5 3 Linear Equation In Two Variables Youtube




X Y 5 X Y 1 Elimination Method Novocom Top
SOLVING SYSTEMS OF EQUATIONS ALGEBRAICALLY How to Use the Elimination Method How to Use the Substitution Method 97 2 x 1 5 x ≥ 0 4 4 4 Simplify both sides of the equation x=3 Substitute 3 in place of x in one of the original equations y = 2x y=2 3 y=6 The solution of the system is (3,6)Modeling Solve the following systems of equations by eliminationX2y = 10 3xy = 0 Math How do I solve these problems, I really need help Solve by substitution method 6x5y=17 x=538y Solve by elimination method 2x3y=5 4x6y=10 Math Algebra 1Solving system of equation by substitution method, involves solving any one of the given equation for either 'x' or 'y' and plugging that in the other equation and solve that equation for another variableSubstitution method questions 2 Step 1 Solve any




7x 3y 1 0



Q Tbn And9gcsiggdhv5fw1mvrwy6npui8oe9vjy7ffnulpwxqmdm604bzyzap Usqp Cau
Watch this video lesson to learn how you can solve a system of linear equations in two variables by using the substitution method Learn how easy it is to use on any linear system in two variables Class 9 Chapter 5 Simultaneous Linear Equation ML Aggarwal Solutions for ICSE is one of the most important chapter for the board exams which is based on solving simultaneous linear equations by substitution method, solving system of simultaneous linear equations by the elimination method, solving expressions of equation and solving simultaneous linear equations by crossmultiplication method Using the Substitution Method to solve systems of Linear Equations In the substitution method a quantity may be substituted for its equal Ex 4x3y=27 and y = 2x 1 4x 3 (2x1) =27 4x 6x 3 =27 10x 3 = 27 10x = 30 x=3



Using Matrices Solve The Following System Of Equations 2x 3y 5z 11 3x 2y 4z 5 X Y 2z 3 Quora




Ssc Mathematics Chapter 4 Pair Of Linear Equations In Two Variables
Free system of equations calculator solve system of equations stepbystepSubstitute the value of y from one equation to other 5–2x=3/2x2 52=3/2x2x 7=7/2x 7*2/7=x 2=x y=5–2*2=5–4=1 x=2,y=1Click here👆to get an answer to your question ️ Solve the equation by substitution method 2x 3y = 9 , 3x 4y = 5




Solving Systems Of Equations Using Linear Combinations




7x 3y 1 0
Substitution method x2y=2x5, xy=3 \square!Since one of the equations has a variable solved for already, lets use substitution The steps in substitution are as follows 1) Solve one of the equations for a variable 2) Plug in the value of that variable into the other equation and solve for the one variable left 3) Plug that value into 1 and solve for the first variableSolve each pair of equation by using the substitution method x(6)/(y)=6 and 3x(8)/(y)=5 Solve for x, y (x^(2)),(y^(2)) 3 (2x),(3y) = (5),(18)




Show That The System Of Equations 2x 5y 17 5x 3y 14 Has A Unique Solution Find The Solution
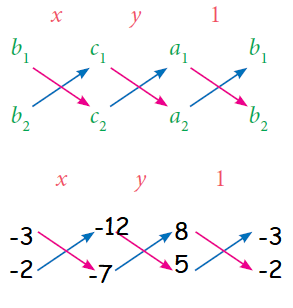



Solving Equations Using Cross Multiplication Method
Solve by substitution method 3x 4y = 10, 2x 2y = 2 Get the answer to this question and access a vast question bank that is tailored for students17) solve this linear system using the method of substitution 2yx=10 y= 3/2x1 ) simplify then solve by substitution 2(x4)y=6 3x2(y3)=13 just need help with these 2 math ALGEBRA Solve by either the substitution method or the addition or subtraction method 2m=n3 3m=2n9 Just replace n with (2m 3) in the second equation Then solve Solve by the substitution method 5x3y=14 x=23y Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled them



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




Algebra Ppt Download
Algebra Solve by Substitution 2x2y=3 , 2xy=5 2x 2y = −3 2 x 2 y = 3 , 2x − y = 5 2 x y = 5 Solve for y y in the second equation Tap for more steps Subtract 2 x 2 x from both sides of the equation − y = 5 − 2 x y = 5 2 x3/2x 2/3y=51 5/x3/y=12 Question on simultaneous linear equation Solve this by reducible to pair of equation method and cross multiplication method MathsWhich method do you use to solve the system of equations #y=1/4x14# and #y=19/8x7#?




5x 3y 1 2x 5y 19 Solve It By The Method Of Substitution Need Answer With Full Method No Brainly In




Practice Problems Mat110 Chapter 9
Here is a problem that has an infinite number of solutions #3x2y= 12# #6x4y=24# If you solve this your answer would be #0=0# this means the problem has an infinite number of solutions For an answer to have no solution both answers would not equal each other Here is a problemSolve by Substitution 2x3y=1 x3y=5 2x − 3y = 1 2 x 3 y = 1 x 3y = 5 x 3 y = 5 Subtract 3y 3 y from both sides of the equation x = 5− 3y x = 5 3 y 2x−3y = 1 2 x 3 y = 1 Replace all occurrences of x x with 5−3y 5 3 y in each equation Tap for more stepsWhat are the 2 numbers if the sum is 70 and they differ by 11?



2




1 Solve The Following Systems Of Linear Equations Chegg Com
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Substitution method 1 See answer Sarah is waiting for your help Add your answer and earn points wikk wikkClick here👆to get an answer to your question ️ Solve the following system of equations by elimination method 8x 3y = 5xy, 6x 5y = 2xy,x = 0,y = 0




Answers




Answered Solve By The Substitution Method Sy Bartleby
Integrate 12x 2 (32x) 5 Take (32x) 5 = (3 2x) 2 (3 2x) 3 Principal algebraic expressions and formulas (ab) 2 = a 2 2abb 2 and (ab) 3 =a 3 3a 2 b3ab 2 b 3 = (9 4x 2 12x)(27 8x 3 54x 18x ) FOIL method the product of two binomials is the sum of the products of the First terms, the Outer terms, the Inner terms and the Last terms




Solve System Of Linear Equations Using Matrix Method 2x 3y 3z 5 X 2y Z 4 3x Y 2z 3 Mathematics Shaalaa Com




Solve The Following Simultaneous Equation By Elimination Method 3x 4y 10 4x 3y 5



The Substitution Method




For What Value A And B The Following System Of Linear Equations Have An Infinite Number Of Solutions 2a 1 X 3y 5 3x B 2 Y 3 Mathematics Topperlearning Com Jafl8e




1 Evaluate 3 X 5 Y For X



2




Solve 2x 3y 11 And 2x 4y 24 And Hence Find The Value Of M For Which Y Mx 3



Solve For X And Y 5 X 3 Y 1 3 2x 2 3y 5 Sarthaks Econnect Largest Online Education Community



1
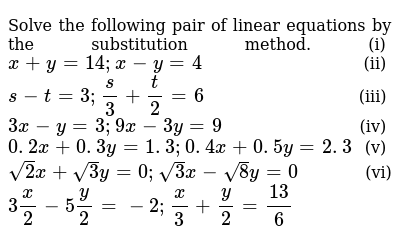



Ncert Solutions For Class 10 Maths Pair Of Linear Equations In Two Variables




5 X 3 Y 1 3 2x 2 3y 5 Brainly In




Solutions Manual For Beginning Algebra 7th Edition By Martin Gay By Cndps109 Issuu



1




3 Systems Of Linear Equations



Solve The Following Simultaneous Equations 5x 3y 8 3x Y 2 Sarthaks Econnect Largest Online Education Community




2 X 2 3y 1 6 2 X 1 Y 1 Solve By Reducing Them To Pairs Of Linear Equations Please Maths Simultaneous Linear Equations Meritnation Com




X 3y 5 3x Y 5 Brainly In




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




2 X 3 3 Y 5 0 5 X 1 4 Y 4 0 Solve It By Substitution Method Brainly In
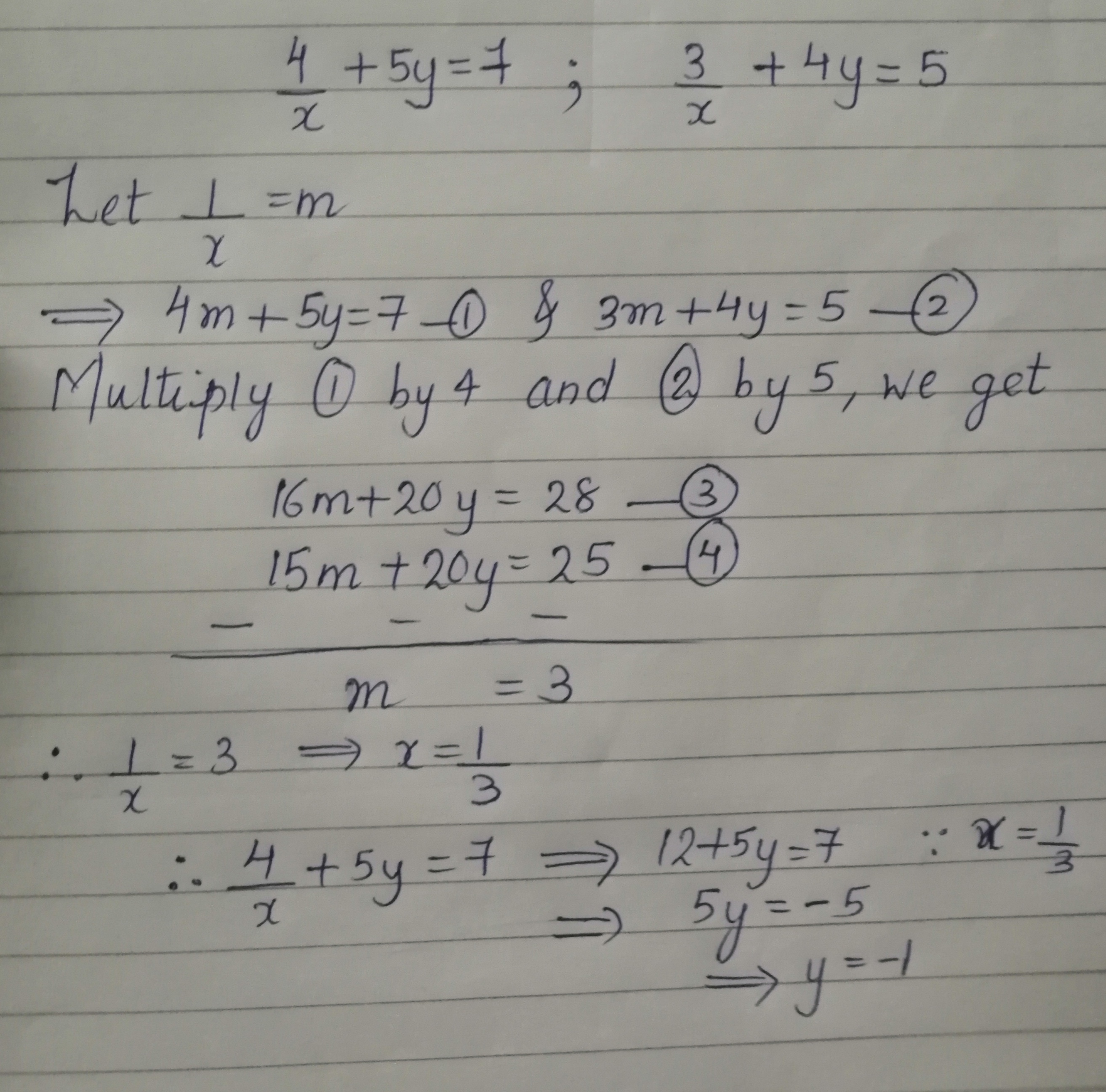



4 X 5y 7 3 X 4y 5 Mathematics Topperlearning Com Eyz2xh55




Solve For X And Y 1 7x 1 6y 3 1 2x 1 3y 5 Brainly In




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




Answered Exercise Set 9 1 S2y3d X 2y 7 Zx Bartleby




5 X 3 Y 1 3 2x 2 3y 5




Frank Chapter 8 Simultaneous Linear Equations Icse Solutions Class 9 Math




1 2 3x 4y 1 5 2x 3y 1 4 Amp 5 3x 4y 2 2x 3y 3 2 Problem Set 1 Q6 5 Youtube




Solve 3x 5y 19 0 And 7x 3y 1 0 By Substituting Method Scholr



Systems Of Linear Equations




5 X 3 Y 1 3 2x 2 3y 5




Vocabulary Chapter Section Topic Simultaneous Linear Equations Ppt Download




If 3x 5y 9 And 5x 3y 7 Then Find The Value Of X Y Youtube
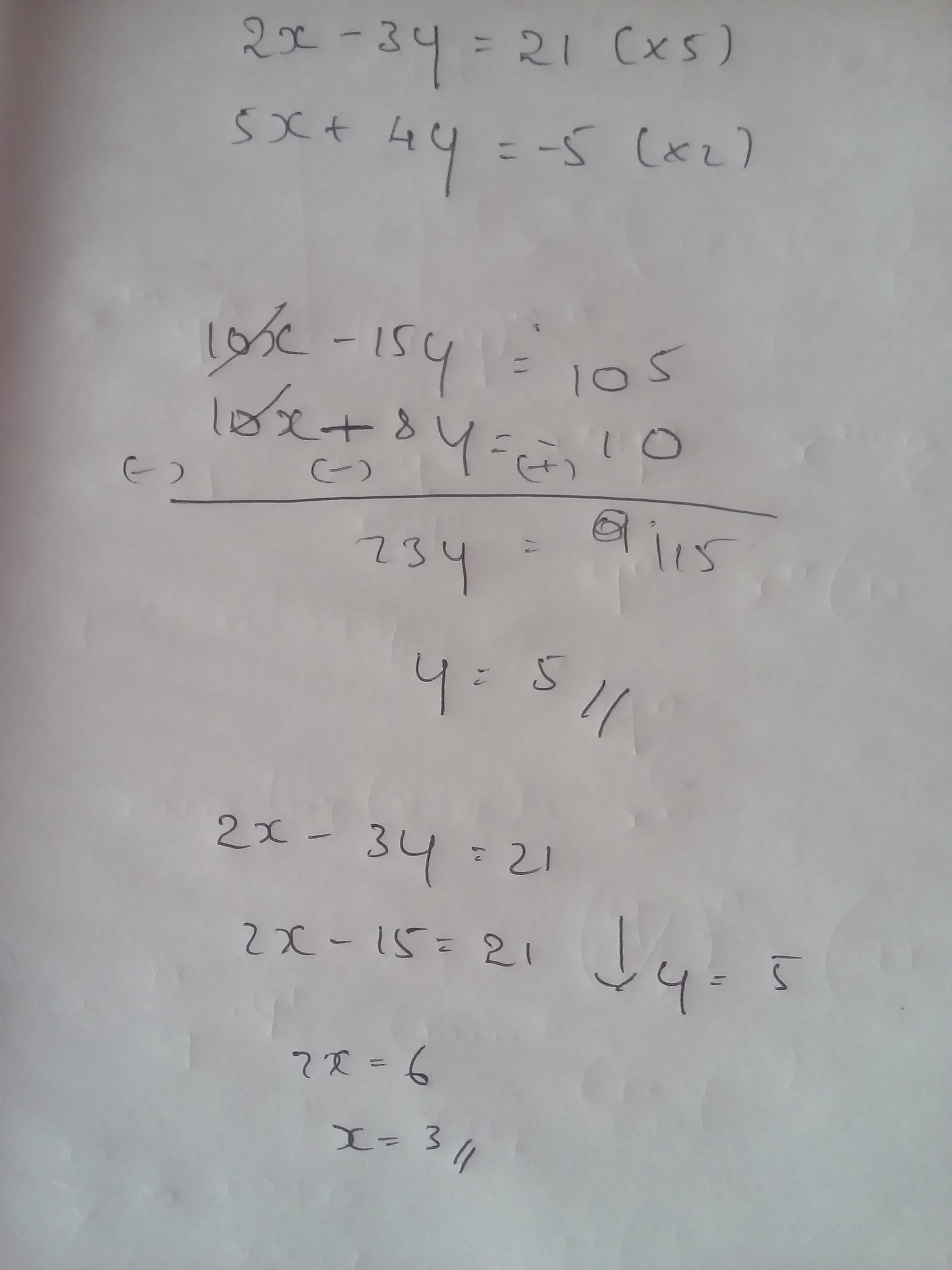



How Do You Solve 2x 3y 21 And 5x 4y 5 Socratic




Solve Each Of The Following Pairs Of Linear Equations By Eliminating X By Substitution 2x 3y 5 0 10x 21y 1 0 Snapsolve
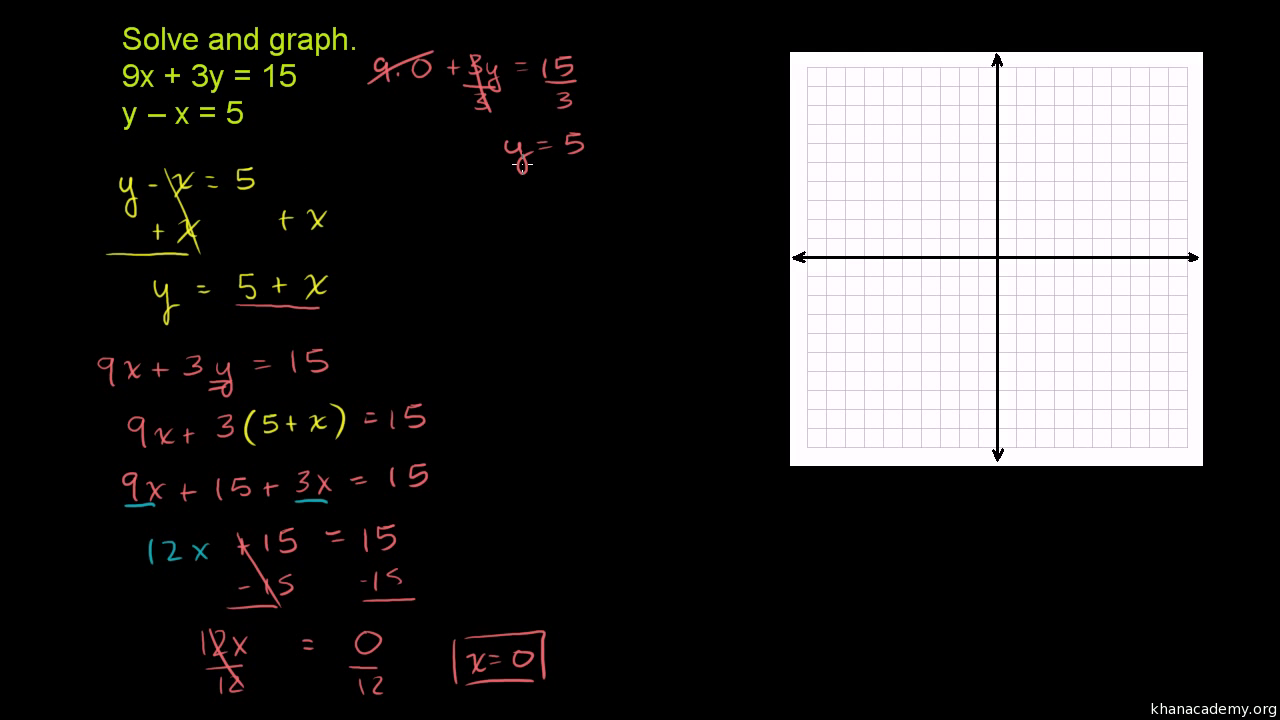



Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy




2x 3y 4 3x Y 5 Solve It By Substitution Method Brainly In



What Is The Answer To Find The Equation Of A Straight Line Through The Point Of Intersection Of Lines 2x 3y 5 0 And 3x 4y 7 0 Which Is Parallel To The Line 2x Y 2 0 Quora
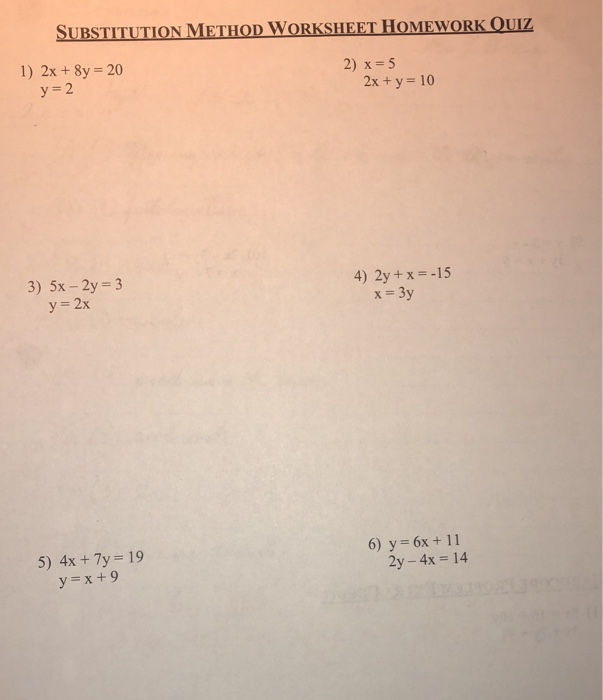



Substitution Method Worksheet Homework Ouiz 1 2x 8y Chegg Com




3 2x 2 3y 5 5 X 3 Y 1 Solve For X And Y Youtube




Solving A System Of Equations Using A Matrix Precalculus Socratic




Solving A System Of Equations Using A Matrix Precalculus Socratic



Q Tbn And9gcqwm8znoo7plhqkc9e5nvkacmtnoafzty4x9md00ol96iaq984o Usqp Cau
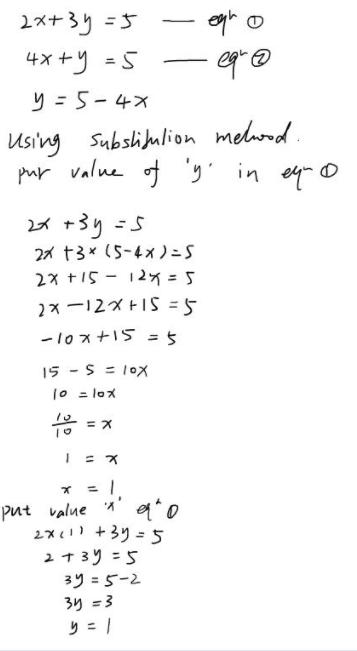



Solve The Following System Of Equations Using The Method Of Substitution 2x 3y 5 4x Y 5 Snapsolve




3 58 Solve The System By Using The Elimination Chegg Com




123a Ppt All 2
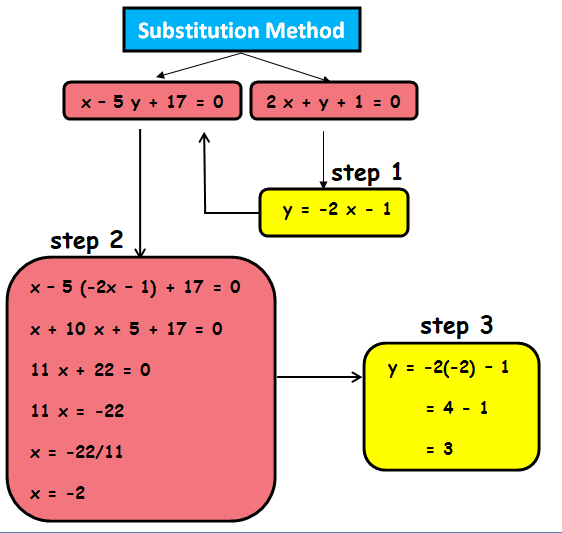



Substitution Method Questions 1




Warm Up Simplify Each Expression 1 3x 2y 5x 2y Ppt Video Online Download




In Problems 7 10 Solve The Systems Of Equations By Chegg Com




5 X 3 Y 1 3 2x 2 3y 5 Find The Value Of X Y By Substitution Method To Be A Brainliest Brainly In
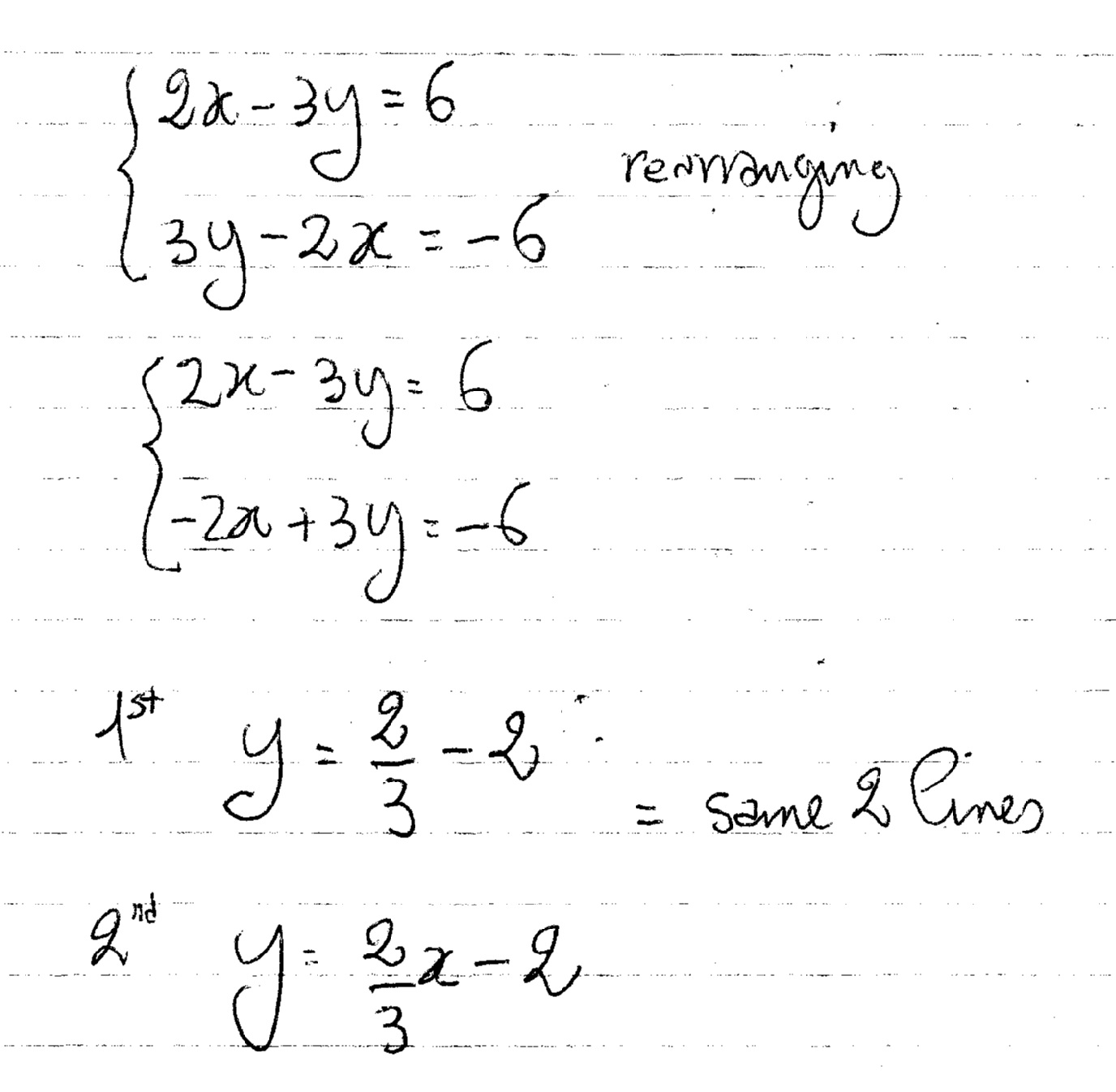



How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic



The Substitution Method




J19



2




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com




Ex 4 6 3 Examine Consistency X 3y 5 2x 6y 8 Ex 4 6




X Y 5 2x 2y 10 Elimination Method Novocom Top
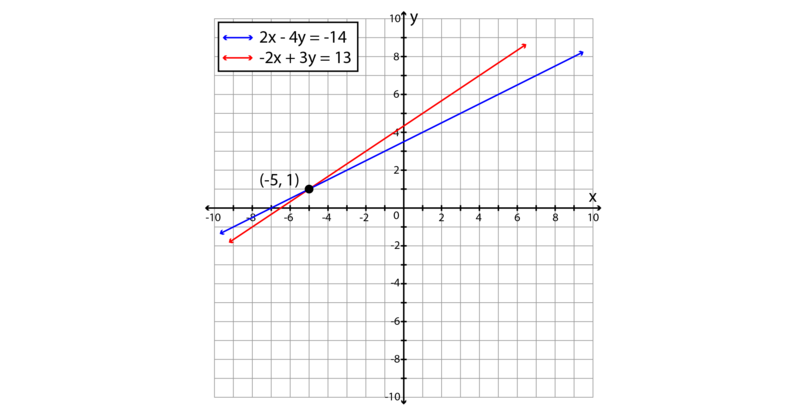



Tables And Graphs Simultaneous Linear Equations Siyavula




5x 3y 8 0 2x 3y 5 0 In Substitution Mothod Brainly In




Show Graphically That The System Of Linear Equations 2x 3y 5 6y 4x 3 Youtube



最も好ましい 5 X 3 Y 1 3 2x 2 3y 5 By Substitution Method




3x 4y 4 2x 3y 2 See How To Solve It At Qanda




By Elimination Method Solve 3 2x 2 3y 5 5 X 3 Y 1 Brainly In



What Is The Value Of X And Y 2x 3y 5 X 2y 1 Quora



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




Graph Graph Inequalities With Step By Step Math Problem Solver




Solve X Y 5 And 2x 3y 4 Novocom Top




Solve The Following Linear Equation By Substitution Method 8x 3y 12 5x 2y 7
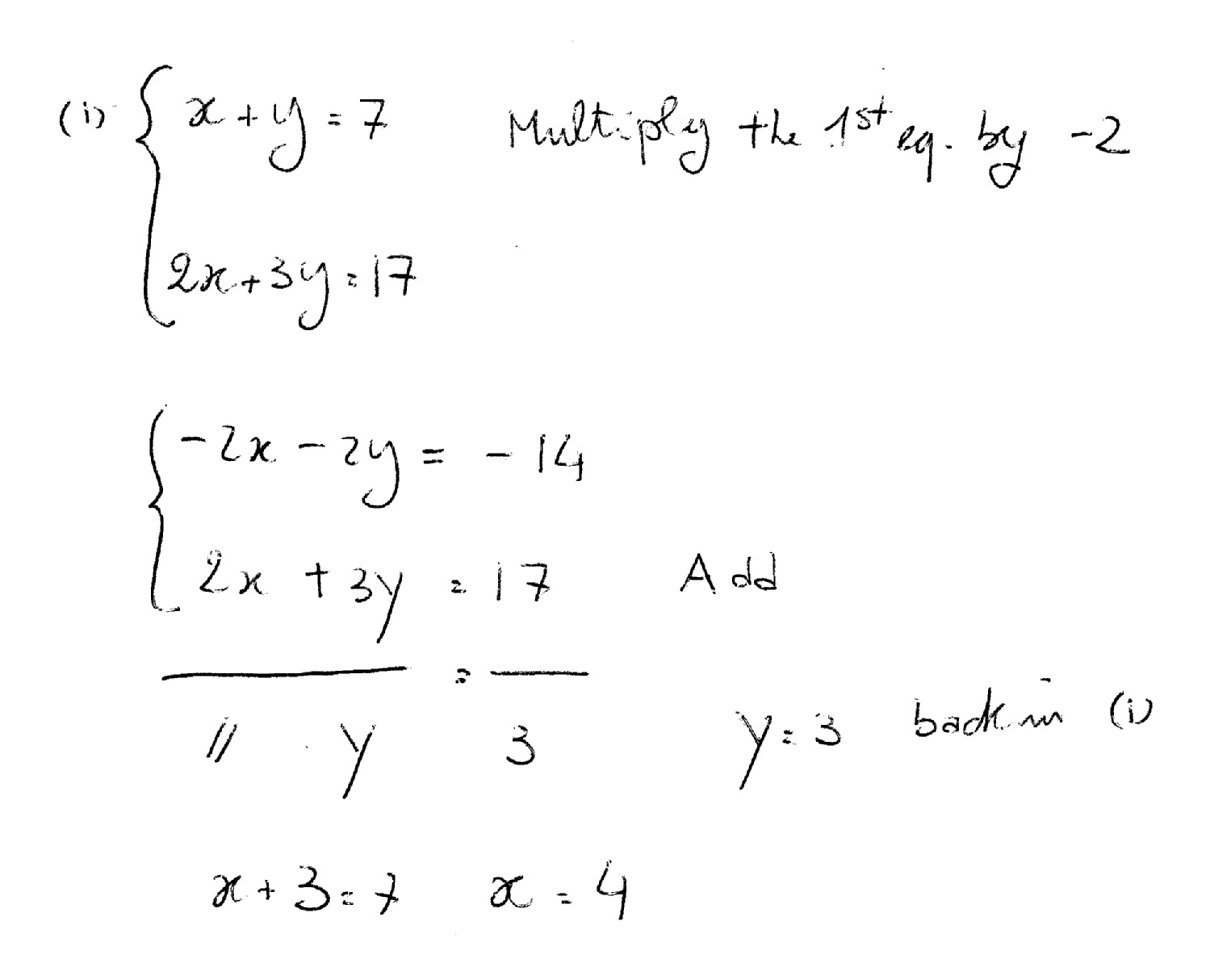



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic



2




3x Y 1 0 2x 3y 8 0 By Elimination Method Novocom Top



How To Solve The Following Equation By Matrix Method 3x 5y 21 And 2x 3y 13 Quora



2




Practice Problems Mat110 Chapter 9
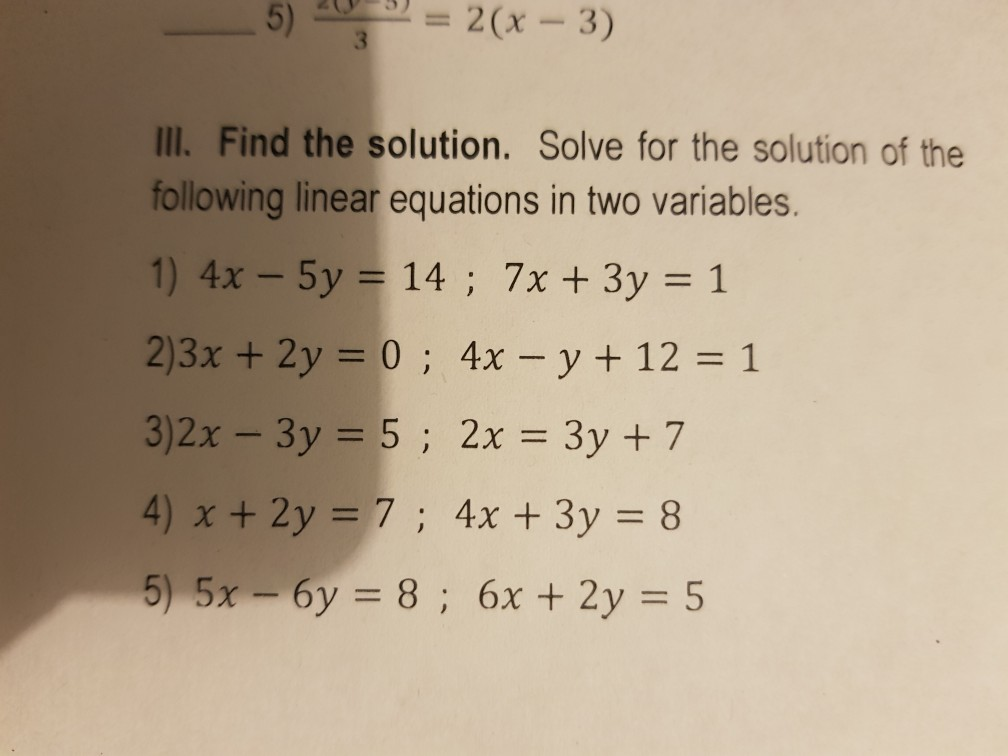



7x 3y 1 0




If The System Of Equations 2x 3y 5 4x K Y 10 Has Infinitely Many Solutions Then Youtube




Let S Learn Solving Systems Using The Substitution Method




無料ダウンロード 3x 2y5 X5 Y


